東京 職業訓練 試験問題[筆記試験] 数学-問2(3)(4)【平成31年1月生】

試験問題 問２(３)

図のように、道路沿いに長方形の土地があります。この土地の道路に面したＡＢ間とＢＣ間に樹木を植えます。等間隔でなるべく少ない本数にするために必要な樹木は何本であるか求めなさい。ただし、３点Ａ、Ｂ、Ｃの３カ所には必ず樹木を植えるものとします。

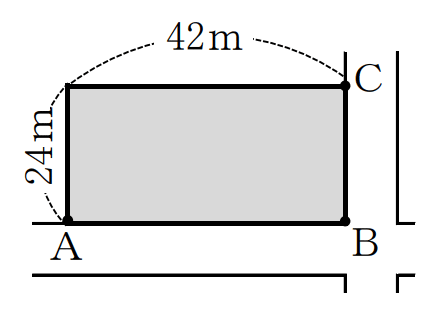
解答と解説

問２(３)の解答：12本

ＡＢ間の樹木の間が42ｍ、ＢＣ間の樹木の間隔が24ｍなので、すくなくても各樹木間の間隔は42と24の約数値であることがわかります。また、できる限り少ない本数にしたいということなので、間隔が最も長くなる最大公約数を求めればいいことになります。

42と24の最大公約数は次の通り。

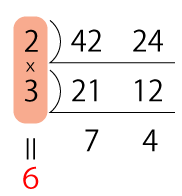
6ｍ間隔で植えるというのが分かったので、次は本数を求めていきます。

ＡＢ間は42ｍあるので、全部で42÷6＋1＝8本植えられます。42÷6＝7本として間違えないようにしてくださいね。

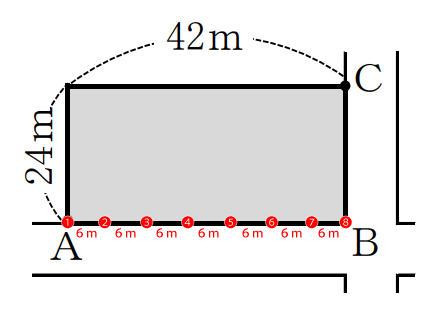
次にＢＣ間は24ｍあるので、全部で全部で24÷6＋1＝5本植えられます。しかし、Ｂ地点の樹木はＡＢ間の方でカウントしているので重複カウントしないようにＢＣ間では数にいれません。よって、4本。

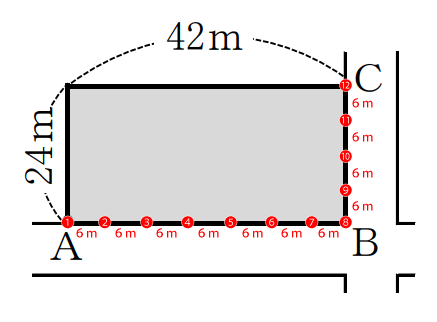
道路沿いに植える樹木は次の通り。

道路沿いに植える樹木＝8本＋4本
　　　　　　　　　　＝12本

試験問題 問２(４)

当たり３本、はずれ７本の合計10本のくじがあります。Ａ君、Ｂ君の順にくじを１本ずつひくとき、Ｂ君の当たる確率を分数で求めなさい。ただし，Ａ君はひいたくじを戻さないこととします。

解答と解説

問２(４)の解答：3/10

この問題は、3/10と瞬時に分かりたい問題です。

10本の中に当たりが3本ある場合、当たる確率はそのままの3/10になります。くじを引く順番で当たる確率は変わりません。もし、当たる確率が変わるのであれば宝くじも当たる確率が高いタイミングで皆、買うようになりますよね。

では、以下の流れで実際に計算で確認していきたいと思います。

Ａ君が当たりＢ君も当たる確率

Ａ君が当たりを引く確率と、Ｂ君が当たりを引く確率は次の通り。

Ａ君が当たりを引く確率＝3/10
Ｂ君が当たりを引く確率＝2/9

よって、Ａ君が当たりＢ君も当たる確率は次の通り。
3/10×2/9＝6/90・・・①

Ａ君が外れ、Ｂ君が当たる確率

Ａ君が外れを引く確率と、Ｂ君が当たりを引く確率は次の通り。

Ａ君が外れを引く確率＝7/10
Ｂ君が当たりを引く確率＝3/9

よって、Ａ君が外れ、Ｂ君が当たる確率は次の通り。
7/10×3/9＝21/90・・・②

合算確率

Ｂ君が当たりを引く場合、『Ａ君が当たりＢ君も当たる』、『Ａ君が外れ、Ｂ君が当たる』の2つのパターンが考えられます。よって、Ｂ君が当たりを引く確率はこの2つのパターンの合算確率となります。その合算確率は次の通り。

合算確率＝①＋②
　　　　＝6/90＋21/90
　　　　＝27/90
　　　　＝3/10

よって、Ｂ君が当たりを引く確率は3/10

※記載している解説の内容に誤りや不明な点があれば遠慮なくコメントください。