このページは平成27年度の広島県の職業訓練校（広島県立技術短期大学校）の推薦入学試験問題の問8の解答と解説を記載しています。三角形の相似条件や比、立体の体積を求める問題ですが、他の都道府県の職業訓練入校試験問題で出題される内容より高い知識が求められています。ただ、毎年出題傾向は同じなので過去問を繰り返し実施して慣れておくようにしてください。

問１～問７に関しては以下のページに解説をまとめているので参考にして下さい。

実際の試験の問題用紙は以下のページで確認することができます。

⇒平成27年度 広島県立技術短期大学校推薦入学試験問題

■目次

  1. 試験問題 問８(１)
  2. 試験問題 問８(２)
  3. 試験問題 問８(３)

試験問題 問８(１)

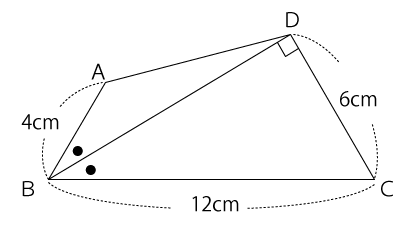
下の図のように、AB＝4cm、BC＝12cm、CD＝6cm、∠ABD＝∠CBD、∠BDC＝90°である四角形ABCDがある。このとき、四角形ABCDの面積を求めなさい。

四角形ABCDの図

解答と解説

問８(１)の解答：24√3

この問題を解くには以下の２点を知っている必要があります。

解くのに必要な知識

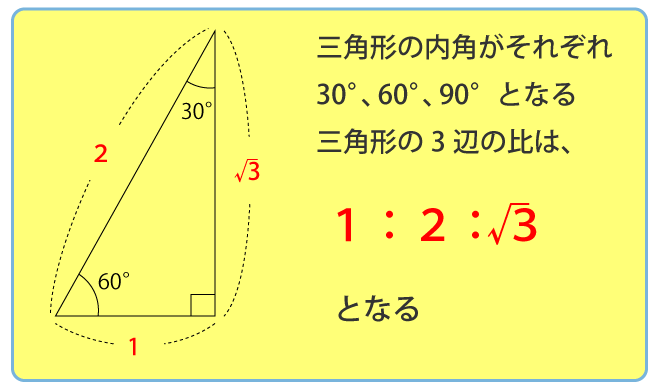
  • 特別な直角三角形の３辺の比
  • 三角形の相似条件

特別な三角形の比

三角形の相似条件

  • 3組の辺の比がすべて等しい
  • 2組の辺の比が等しく、その間の角が等しい
  • 2組の角がそれぞれ等しい

△BCDは直角三角形で、辺CDと辺BCの比が1：2になっています。よって、この直角三角形は特別な直角三角形の３辺の比が適用できることが分かります。

CD：BC：BD＝1：2：√3
6：12：BD＝1：2：√3

BD＝6√3

次に点Aから辺BDに対して垂線を引き、その交点をＥとします。

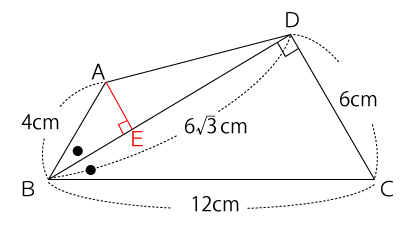
相似な三角形

そうすると、∠BDC＝∠BEA＝90°、∠ABE＝∠CBDなので三角形の相似条件『2組の角がそれぞれ等しい』を満たすので、△ABEと△CBDは相似な三角形だと分かります。その比は次の通り。

CD：BC＝AE：BA
6：12＝AE：4
AE＝2

これで△ABDの高さが分かりました。

△ABDの面積＝6√3×2÷2
　　　　　＝6√3

△BCDの面積＝6×6√3÷2
　　　　　＝18√3

よって、四角形ABCDの面積は次の通り。

四角形ABCDの面積＝6√3＋18√3
　　　　　　　　＝24√3

試験問題 問８(２)

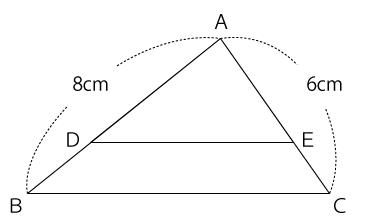
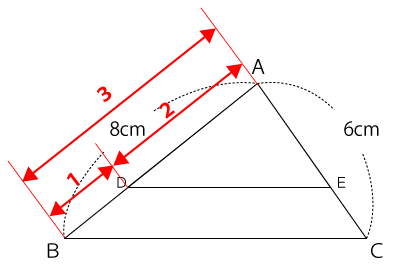
下の図のように、AB＝8cm、CA＝6cm、△ABC＝18cm²である△ABCがある。辺AB、辺AC上に、それぞれAD：DB＝AE：EC＝2：１となる点D、Eをとるとき、台形BCEDの面積を求めなさい。

三角形と比

解答と解説

問８(２)の解答：10cm²

△ABCと△ADEは、三角形の相似条件『2組の辺の比が等しく、その間の角が等しい』を満たしており、相似な三角形だと分かりますAD：DB＝AE：EC＝2：１なのでこの2つの三角形の相似比は次の通りになります。

△ABC：△ADE＝3：2・・・①

相似な三角形

辺BCの長さをＮcm、点Aから辺BCに垂線を下ろしDEと交わる点をF、BCと交わる点をG、AGの長さをＭcmとすると下図のようになります。

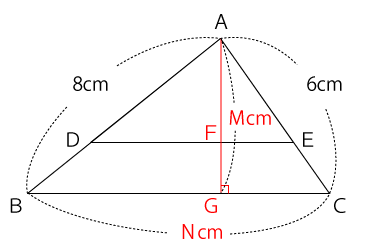
相似な三角形の面積

△ABCの面積は問題文より18cm²と分かっているので以下の式が成り立ちます。

Ｎ×Ｍ÷2＝18
ＮＭ＝36・・・②

①より、『AF：AG＝DE：BC＝2：3』が成り立つので、AFとDEの長さは次のようにあらわすことができます。

AF：AG＝2：3
2AG＝3AF
AF＝23AG
AF＝2Ｍ3

DE：BC＝2：3
2BC＝3DE
DE＝23BC
DE＝2Ｎ3

よって、△ADEの面積は次の通り。

△ADEの面積＝2Ｍ3×2Ｎ3÷2
　　　　　＝2ＭＮ9・・・②

②よりＭＮ＝36なので△ADEの面積は次の通り。

△ADEの面積＝2×369
　　　　　＝8cm²

よって、台形BCEDの面積は次の通り。

台形BCEDの面積＝△ABCの面積－△ADEの面積
　　　　　　　＝18－8
　　　　　　　＝10cm²

別の解き方

この問題は三角形の相似比と面積比の関係を知っていれば簡単に解くことができます。

相似比と面積比の関係

①より、△ABCと△ADEの相似比は、『△ABC：△ADE＝3：2』だと分かっています。よって、面積比は次の通りになります。

△ABC面積：△ADE面積＝3²：2²

問題文より△ABCの面積は18cm²と分かっているので、△ADEの面積は次の通りになります。

△ABC面積：△ADE面積＝3²：2²
18：△ADE面積＝9：4
△ADE面積×9＝18×4
△ADE面積＝18×4÷9
　　　　　＝8cm²

よって、台形BCEDの面積は次の通り。

台形BCEDの面積＝△ABCの面積－△ADEの面積
　　　　　　　＝18－8
　　　　　　　＝10cm²

試験問題 問８(３)

下の図のように、体積が270cm³である円すいを底面に平行な平面で切り、P、Q、Rの３つの部分に分けるとき、Rの体積を求めよ。

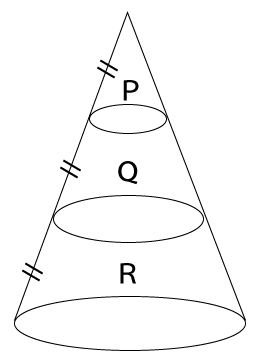
円すいの図

解答と解説

問８(３)の解答：190cm³

相似な図形の相似比と体積比は以下の関係が成り立ちます。前問の相似比と面積の関係と合わせて覚えておくようにしましょう。

相似な図形の相似比と体積比の関係

円すいPQと円すいPQRは相似な円すいでその比はPQ：PQR＝2：3となります。

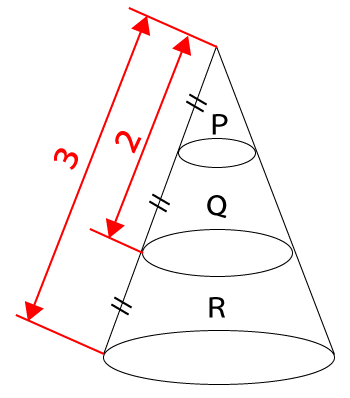
相似な円すいの図

相似な図形の相似比と体積比の関係より、以下の式が成り立ちます。

PQの体積：PQRの体積＝2³：3³

問題文からPQRの体積は270cm³と分かっているのでPQの体積は次の通り。

PQの体積：270＝8：27
PQの体積×27＝2160
PQの体積＝2160÷27
　　　　＝80cm³

よって、Rの体積は次の通り。

Rの体積＝270－80
　　　＝190cm³

※記載している解説の内容に誤りや不明な点があれば遠慮なくコメントください。