大阪 職業訓練 試験問題 数学-問4(平成30年8月24日実施) 短期課程

問４ 試験問題

下の図のように△ABCのABを1：2の比に分ける点をD、ACの中点をE、CDとBEの交点をFとするとき、以下の問いの答えとして正しいものをア～オの中から１つ選び、記号で答えなさい。

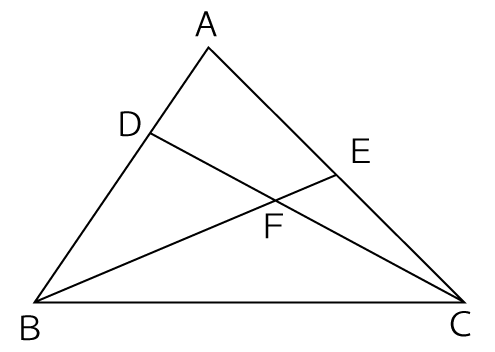
[問題1]　DF：FC を簡単な比で表せ。

[問題2]　△ABCの面積が10のとき、△FBCの面積を求めよ。

解答と解説

解答と解説を記載していきます。
解き方が分からないという人を少しでも減らすためにできる限り分かり易く必要以上に細かく順を追って解説している部分がありますが、実際の試験時は丁寧に計算し過ぎると時間のロスに繋がるため、自分の分かるところは効率よく解答していくようにしてください。

問題１の解答と解説

試験問題１の解答：イ

この問題を解くには、三角形の相似条件を知っている必要があります。

下図のように辺ACと平行な線分DGを引きます。

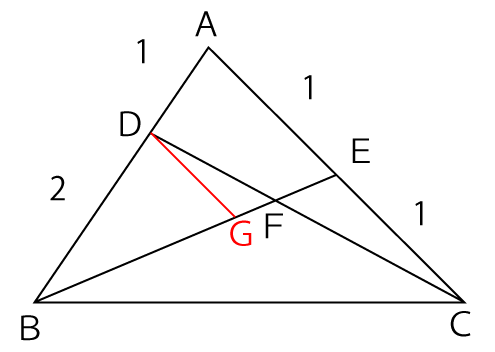
すると、三角形DBGと三角形ABEは3組の角が等しいので相似な三角形と言えます。そして、その相似比は次の通り。

△DBG：△ABE＝2：3

よって、辺DGと辺AEの比も次の通りになります。

辺DG：辺AE＝2：3

次に三角形FDGと三角形FCEに着目すると、この2つの三角形も3組の角がそれぞれ等しいので相似な三角形になります。そして、その比は次の通りになります。

辺DG：辺AE＝2：3
辺DG：(辺AE＝辺CE)＝2：3
辺DG：辺CE＝2：3

よって、

△FDG:△FCE＝2：3

これにより、求めたい辺DFと辺FCも2:3となります。

DF:FC＝2：3

問題２の解答と解説

試験問題２の解答：ウ

この問題を解くには、三角形の面積比のルールを知っている必要があります。

まず、頂点AからFに線分AFを引き、△AFC(黄色部分)と△BFC(青色部分)の面積比を求めます。

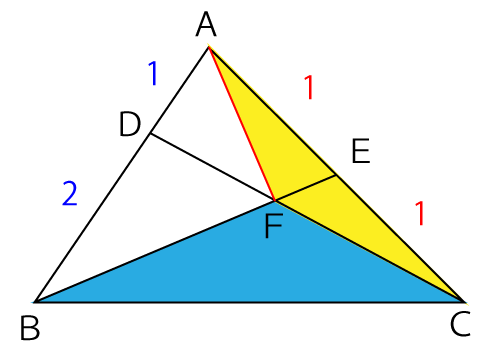
上の図を見て瞬時に面積比は『△AFC：△BFC＝1：2』だと分かった人は優秀です。では、なぜ『△AFC：△BFC＝1：2』となるのかを解説していきます。

△ADCと△BDCは高さが共通な三角形になります。これは分かりますでしょうか？
下図のように頂点Cから辺ABに垂線を引き、交わる点をｈとした場合、線分Chが△ADCと△BDCの高さになります。

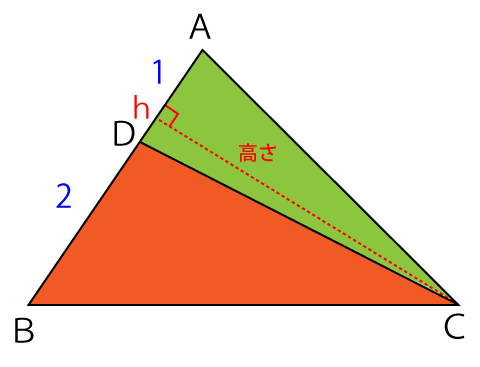
よって、三角形の面積比のルール１『異なる2つの三角形の高さが同じである場合、面積比は底辺の長さの比に等しい』により、△ADCと△BDCの面積比は『△ADC：△BDC＝1：2』となります。

次に同様に△ADFと△BDFの面積比を見ていきます。

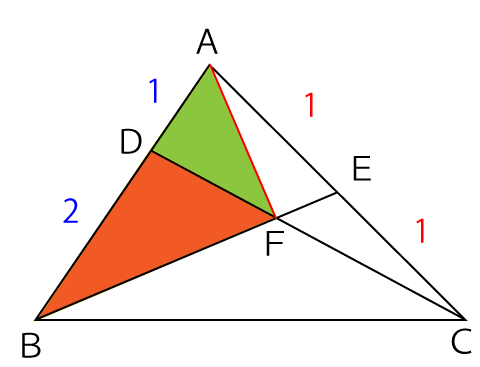
この2つの三角形に関しても先ほどと同じで、高さが同じ三角形なので三角形の面積比のルール１『異なる2つの三角形の高さが同じである場合、面積比は底辺の長さの比に等しい』により、△ADFと△BDFの面積比は『△ADF：△BDF＝1：2』となります。

よって、面積比が1:2の△ADCと△BDCから、面積比が1：2の△ADFと△BDF部分を取り除いても△AFCと△BFCの面積比は変わりません。よって、『△AFC：△BFC＝1：2』となります。

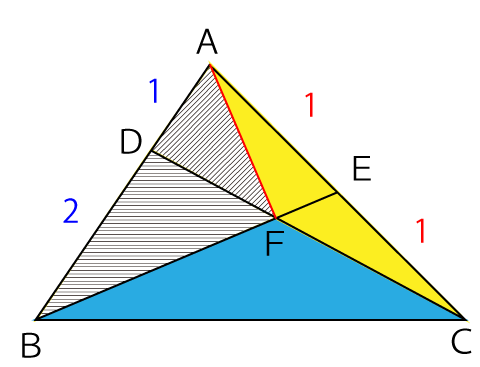
次に△ABFと△BFCの面積比を見ていきます。先ほどと同じ理由で、この2つの面積比は『△ABF：△BFC＝1：1』だと瞬時に分かりますよね。分からない方は、これまでの解説をもう一度読み直してみてください。

ここまでを整理すると△AFCと△ABFと△BFCの面積比は次の通りです。

△AFC：△BFC＝1：2
△ABF：△BFC＝1：1

よって、3つの三角形は次の面積比が成り立ちます。

△AFC：△ABF：△BFC＝1：2：2

△ABCはこの3つの三角形を合わせてものなので、△ABCと△BFCの面積比は次のようになります。

△ABC＝△AFC+△ABF+△BFC＝5
△ABC：△BFC＝5：2

よって、三角形ABCの面積が10のとき、三角形BFCの面積は4となります。

※解説を記載するまでもないと判断した問題に関しては、解説を記載せず解答のみを記載しています。もし、この問題の解説が欲しいというのがあれば、コメント欄に記載してください。また、記載している解説の内容に誤りや不明な点があれば遠慮なくコメントください。