大阪 職業訓練 試験問題 数学-問3(平成30年8月24日実施) 短期課程

問３ 試験問題

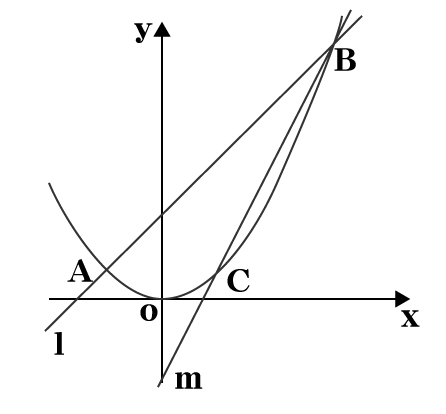
下の図のように放物線ｙ＝ａｘ²と2直線l 、mがそれぞれ2点A、BとB、Cで交わっている。点Aの座標は（－2、1）、点Bのx座標が6、点Cのx座標が2である。以下の問いの答えとして正しいものをア～オの中から１つ選び、記号で答えなさい。

[問題1]　ａの値を求めよ。

[問題2]　直線ｍの式を求めよ

[問題3]　直線lとy軸との交点をDとすると、△OADをy軸を回転の軸として回転させてできる立体の体積を求めよ。

解答と解説

解答と解説を記載していきます。
解き方が分からないという人を少しでも減らすためにできる限り分かり易く必要以上に細かく順を追って解説している部分がありますが、実際の試験時は丁寧に計算し過ぎると時間のロスに繋がるため、自分の分かるところは効率よく解答していくようにしてください。

問題１の解答と解説

試験問題１の解答：ア

点Aの座標が（－2、1）なので、放物線の式に代入し、係数ａの値を求めていきます。

ｙ＝ａＸ²
1＝ａ×(-2)²
1＝4ａ
ａ＝14

問題２の解答と解説

試験問題２の解答：イ

問題１より、放物線の式はｙ＝14ｘ²だと分かりました。

また、点Ｂは放物線上にあり、設問よりｘ座標は6だと分かっているので点Ｂのｙ座標は次の通りになります。

ｙ＝14ｘ²
　＝14×6²
　＝14×36
　＝9

よって、点Ｂの座標は（6、9）

同様に点Ｃのｘ座標は設問より2だと分かっているのでｙ座標は次の通り。

ｙ＝14ｘ²
　＝14×2²
　＝14×4
　＝1

よって、点Ｃの座標は（2、1）

直線の式はｙ＝ａｘ+ｂなので、点Ｂ，点Ｃの座標値を代入し直線ｍの式を求めていきます。

直線ｍは点Ｂを通ることより以下の式が成り立ちます。
ｙ＝ａｘ+ｂ
9＝6ａ+ｂ・・・①

直線ｍは点Ｃを通ることより以下の式が成り立ちます。
ｙ＝ａｘ+ｂ
1＝2ａ+ｂ・・・②

①-②をしてａの値を求めます。
9-1＝(6ａ+ｂ)－(2ａ+ｂ)
8＝4ａ
ａ＝2

このａの値を式①もしくは式②に代入しｂの値も求めていきます。

1＝2ａ+ｂ・・・②
1＝2×2+ｂ
1＝4+ｂ
ｂ＝-3

よって、直線ｍの式は次の通り。

ｙ＝2ｘ-3

問題３の解答と解説

試験問題３の解答：オ

今回求めたいのは下図のオレンジ色部分の立体の面積です。

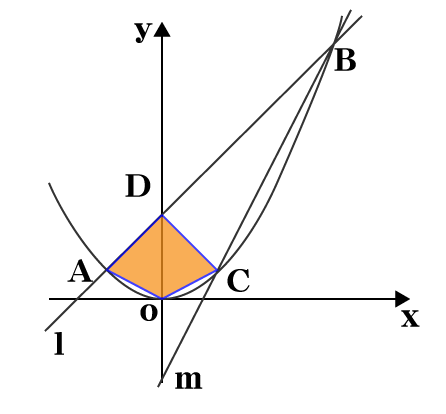
平面図では分かり難いですが、そろばんの玉のような図形です。

体積の求め方は、下図のように立体を線分ＡＣで切り、2つの円すいを作ったのち、2つの円すいの体積をそれぞれ求め最後に合計することで求めていきます。

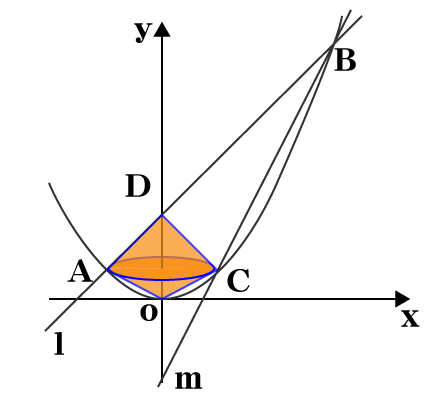
直線ｌが通る2点、点Ａと点Ｂの座標はそれぞれ点Ａ(-2、1)、点Ｂ(6、9)と分かっているので直線のｌの式を求めていきます。

直線lは点Ｂを通ることより以下の式が成り立ちます。
ｙ＝ａｘ+ｂ
9＝6ａ+ｂ・・・③

直線lは点Ａを通ることより以下の式が成り立ちます。
ｙ＝ａｘ+ｂ
1＝-2ａ+ｂ・・・④

③+④×3をしてｂの値を求めます。

9+1×3＝(6ａ+ｂ)+(-2ａ+ｂ)×3
12＝4ｂ
ｂ＝3

ｂは直線ｌの切片、いわゆるｙ軸との交点座標なので、点Ｄの座標は(0、3)だとわかります。

ここまでわかった点を図形に書き込んでみます。

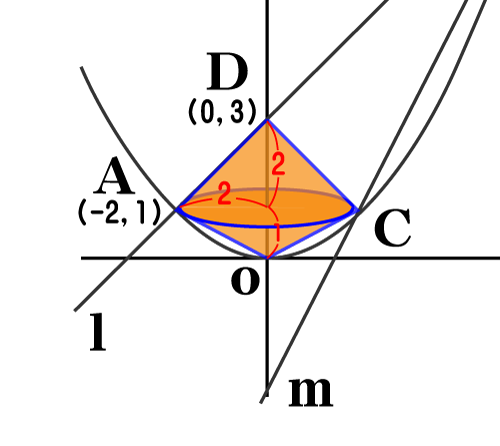
円すいの体積を求める公式は次の通り。

点Dが頂点となる円すいの体積
＝底面積×高さ×13
＝(2×2×π)×2×13
＝8π3

点Oが頂点となる円すいの体積
＝底面積×高さ×13
＝(2×2×π)×1×13
＝4π3

よって、求めたい図形の体積は次の通り。

8π3+4π3
＝12π3
＝4π

※解説を記載するまでもないと判断した問題に関しては、解説を記載せず解答のみを記載しています。もし、この問題の解説が欲しいというのがあれば、コメント欄に記載してください。また、記載している解説の内容に誤りや不明な点があれば遠慮なくコメントください。