平成27年入校 広島県立技術短期大学校 試験問題6 解答

平成27年入校 広島県立技術短期大学校 試験問題の問6の解答です。三角比、三角比の相互関係、三角関数の知識が問われる問題です。三角関数の基本的な値は頭に入れておかなければ解けません。他府県の職業訓練の選考試験問題では出題されないくらいのレベルの高さですね。

問１～問５、問７、問８に関しては以下のページに解説をまとめているので参考にして下さい。

• 試験問題-問１
• 試験問題-問２
• 試験問題-問３
• 試験問題-問４
• 試験問題-問５
• 試験問題-問７
• 試験問題-問８

６. 次の各設問に答えなさい。

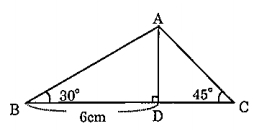
[問題1]　下の図について、辺ＣＡの長さを求めなさい。

[問題2]　tanθ＝－1 のとき、θの値を求めなさい。ただし、0°＜θ＜180° とする。

[問題3]　cosθ＝1/3 のとき、cosθ/(1－sinθ) ＋ cosθ/(1＋sinθ)の値を求めなさい。

解答と解説

試験問題１の解答：2√6
三角関数の下記の表は頭に入れておきたい。

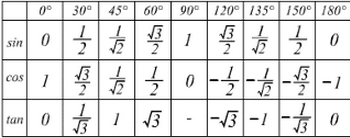
更に三角比についても覚えておきましょう。

　辺ＡＤ＝tan30° × 辺ＢＤ

　tan30°＝1√3
　辺ＢＤ＝6

よって、

　辺ＡＤ＝6√3

三角形ＡＤＣは直角二等辺三角形なので、次の三角比が利用できます。

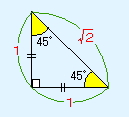
よって、辺ＣＡは、

　辺ＣＡ＝6√3 × √2
　　　　＝6√2√3
　　　　＝6√2√3√3√3
　　　　＝6√63
　　　　＝2√6

別の解き方
先程は、三角関数を使った解き方で解説しましたが、三角比だけで解いた方がよりかと思います。

特別な三角形の比として、以下の2つがあります。45°、45°、90°の直角二等辺三角形の比は先程も使いましたね。

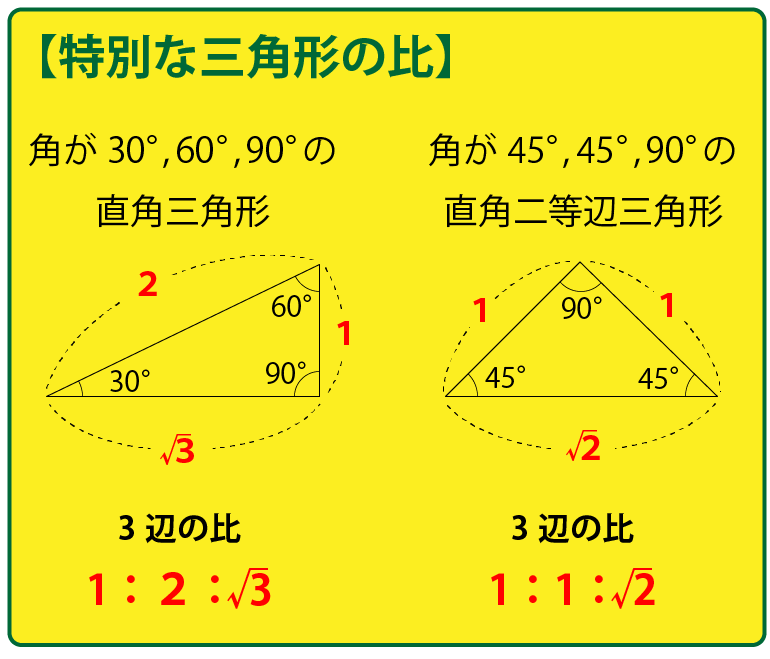
よって、今回の問題であれば、下図のような各辺の比が成り立ちます。

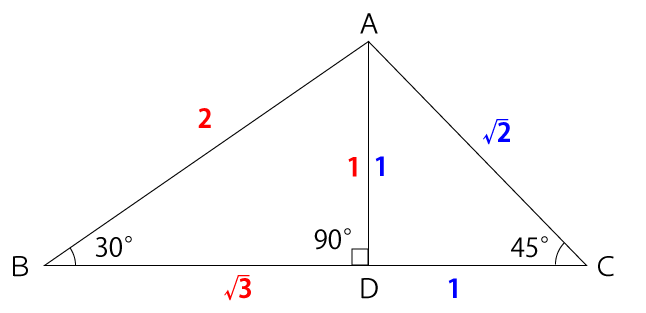
辺ADとBDは以下の比が成り立ちます。
AD：BD＝1：√3

BD＝6cmなのでADの長さは次のようになります。
AD：BD＝1：√3
AD：6＝1：√3
√3AD＝6
AD＝6√3

次にADとACの辺の比は次の通り。
AD：AC＝1：√2

ADの長さは、6√3なので、ACの長さは次のようになります。
AD：AC＝1：√2
6√3：AC＝1：√2
AC＝6√2√3
　＝6√2√33
　＝2√6

試験問題２の解答：135°
この問題は、下の表が頭に入っていれば瞬時に解ける問題ですね。

tanθ＝－1のときは、上記表よりθ＝135°

試験問題３の解答：6
三角比の相互関係を知っている必要があります。これは、数Ⅰで習う問題ですね。

三角比の相互関係で次のようなものがあります。

　sin²θ＋cos²θ＝1

これを利用し、cosθ＝1/3 のときのsinθを求めます。

　sin²θ＋cos²θ＝1
　sin²θ＋(1/3)²＝1
　sin²θ＋1/9＝1
　sin²θ＝1－1/9
　sin²θ＝9/9－1/9
　sin²θ＝8/9
　sinθ＝√8/9
　sinθ＝√2²×2/3²
　sinθ＝2√2/3

よって、cosθ/(1－sinθ) ＋ cosθ/(1＋sinθ)の値は次の通りです。

　　cosθ/(1－sinθ) ＋ cosθ/(1＋sinθ)の値
　＝(1/3)/(1－2√2/3)＋(1/3)/(1＋2√2/3)

なんかよくわからないような形になってしまいましたが、分母、分子に3を掛けてもう少し見やすく変形します。

　＝1/(3－2√2)＋1/(3＋2√2)
　＝{(3＋2√2)＋(3－2√2)} / (3－2√2)(3＋2√2)
　＝6 / (9－4√2²)
　＝6 / (9－4×2)
　＝6 / 1
　＝6