平成27年入校 広島県立技術短期大学校 試験問題の問7の解答です。余弦定理、三角関数の知識が問われる問題です。余弦定理、三角関数に入れておかなければ解けません。他府県の職業訓練の選考試験問題では出題されないくらいのレベルの高さですね。
問1~問6、問8に関しては以下のページに解説をまとめているので参考にして下さい。
7. 次の各設問に答えなさい。
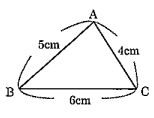
[問題1] △ABCにおいて、AB=5cm、BC=6cm、CA=4cmのとき、cos∠ABCの値を求めなさい。
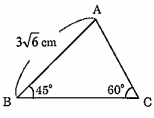
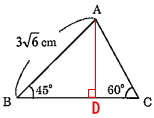
[問題2] △ABCにおいて、AB=3√6cm、∠ABC=45°、∠BCA=60°のとき、辺CAの長さを求めなさい。
解答と解説
試験問題1の解答:3/4
余弦定理を使用します。
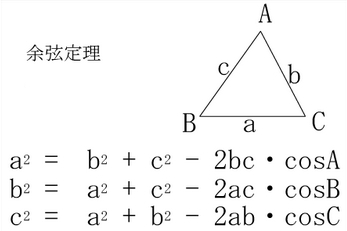
cos∠ABCを求めたいので、使用する余弦定理は下記。
b²=a²+c²-2ac・cos∠ABC
各値を代入します。
4²=6²+5²-2×6×5×cos∠ABC
16=36+25-60cos∠ABC
60cos∠ABC=36+25-16
60cos∠ABC=45
cos∠ABC=45/60=3/4
試験問題2の解答:6cm
三角関数を利用します。下表は、頭にいれておきましょう。
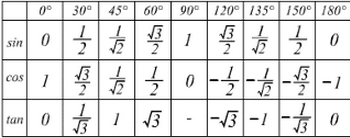
△ABCの頂点Aから辺BCへ垂直に下ろし、辺BCと交わる点をDとします。
sin45°=AD / 3√6
1/√2==AD / 3√6
AD=(1 / √2) × (3√6)
AD=(3√6) / (√2)
AD=3√3
sin60°=AD / CA
√3 / 2 = 3√3 / CA
CA=3√3 × (2 / √3)
CA=6

