次の各設問の解答を答えなさい。
[問題1]
Xの2次方程式X²-mX-2m²=0 ・・・(イ) がX=-1を解に持つとき、次の各設問に答えなさい。
(1)定数mの値を求めなさい。
①1/2 ②3/2 ③1 ④2
(2)2次方程式(イ)の他の解を求めなさい。
①-2 ②1/2 ③1 ④2
[問題2]
2次関数y=x²+3mx+(1/4)m²+2m+4 ・・・(ロ) について、次の各設問に答えなさい。
(1)m=2のとき、2次関数(ロ)のグラフの頂点の座標を求めなさい。
①(-3, 0) ②(-3, 2) ③(3, -1) ④(3, 0)
(2)2次関数(ロ)がX軸と異なる2点で交わるとき、mの値の範囲を求めなさい。
①m<-2, m>1 ②m<-1, m>2 ③-2<m<1 ④-1<m<2
(3)m=4のとき、2次関数(ロ)はX軸と2点で交わる。このとき、この放物線がX軸から切り取る線分の長さを求めなさい。
![]()
解答と解説
試験問題1の解答:
(1)定数mの値を求めなさい。
X=-1を解に持つという事なので、X=-1を2次方程式に代入します。
1+m-2m²=0
2m²-m-1=0
ここでmの2次方程式が出てきたので、この2次方程式をたすき掛けを使って解きます。
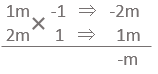
(m-1)(2m+1)=0
よって、m=1、-1/2
しかし、解答群の選択肢にはm=1しかないので、求めたい解答はm=1の③となる。
(2)2次方程式(イ)の他の解を求めなさい。
(1)の解答より、m=1となるので2次方程式(イ)は、X²-X-2=0になる。これを同様にたすき掛けで解くと次のようになる。
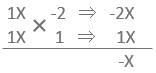
(X-2)(X+1)=0
よって、X=-1、2
X=-1は、既に分かっているので、求めたい他の解は2の④となる。
試験問題2の解答:
(1)m=2のとき、2次関数(ロ)のグラフの頂点の座標を求めなさい。
m=2を2次関数に代入すると次のようになる。
y=X²+6X+1+4+4
y=X²+6X+9
この2次関数の頂点の座標を求める分けだが、4つの解答群の座標を実際に上記の2次関数に代入してみると、①の(-3, 0)しか成り立たないことがわかる。よって、①が正解になるのだが、頂点は求められるようにしておきましょう。
y=X²+6X+9
これを変形させると下記のようになる。
y=(X+3)²+0
よって、頂点は、原点(0, 0)をX軸方向に-3、Y軸方向に0移動させた点になる。このことより、求める解答は(-3, 0)の①となる。
(2)2次関数(ロ)がX軸と異なる2点で交わるとき、mの値の範囲を求めなさい。
X軸と異なる2点で交わるということは、Y=0のときにグラフは、X軸と2ヵ所で交わることを意味する。下のグラフで言うと①になる。
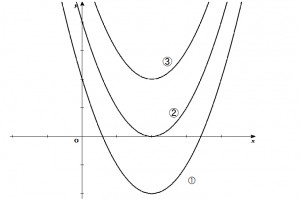
2次関数のグラフが③のようにX軸と交わらない、②のように1点だけ交わる、①のように2ヵ所で交わるかを調べる為には、判別式を利用する。この判別式は覚えておく必要がある。
2次関数y=ax²+bx+cのとき、b²-4acのことを判別式という。このb²-4acが0よりも大きいかどうかで①②③を判別することができる。
b²-4ac>0のとき、X軸と2ヵ所で交わる。
b²-4ac=0のとき、X軸と1ヵ所で交わる。
b²-4ac<0のとき、X軸と交わらない。
これを今回の2次関数y=x²+3mx+(1/4)m²+2m+4 にあてはめると、
a=1
b=3m
c=(1/4)m²+2m+4
よって、判別式b²-4acは、
(3m)²-4x1x{(1/4)m²+2m+4}
9m²-m²-8m-16
8m²-8m-16
となる。今回の設問ではX軸と異なる2点で交わるということなので、この判別式が0より大きくならなければならない。よって、次の不等式が成り立つ。
8m²-8m-16>0
この不等式を解けば、求めたい解が導ける。
8m²-8m-16>0
m²-m-2>0
(m-2)(m+1)>0
よって、求める解答は、m<-1、m>2 の②。
aX²+bX+c<0 (a>0) ⇒ α<X<β
aX²+bX+c>0 (a>0) ⇒ X<α,β<X
(3)m=4のとき、2次関数(ロ)はX軸と2点で交わる。このとき、この放物線がX軸から切り取る線分の長さを求めなさい。
m=4を2次関数に代入すると、『y=X²+12X+16』となる。
求めたい長さは、下図の赤線部分なので、まずはグラフがX軸と交わる2点の座標を求める。
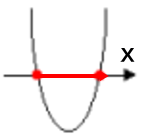
y=0のときのX座標をもとめるので、
y=X²+12X+16
0=X²+12X+16
ここで解の公式を使用して解いてもよいが次のような解き方の方が早い。
X²+12X+16=0
(X+6)²-20=0
(X+6)²=20
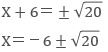
2点の距離を求めるのは、X座標の大きい方から小さい方を引けばいいので、
![]()
よって、求める解答は②となる。

