問1~2、問4に関しては以下のページに解説をまとめているので参考にして下さい。
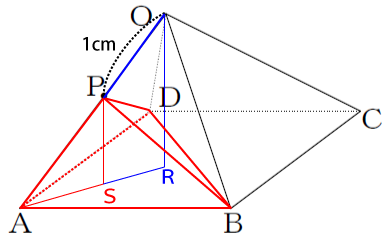
図のようにすべての辺の長さが4cm の正四角すいOABCD がある。以下の問いにア~オから選んで答えなさい。
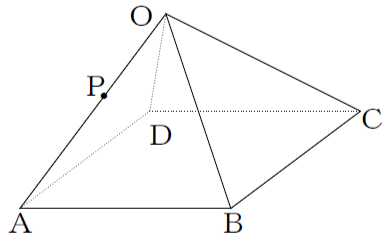
[問題1] △OADの面積を求めなさい。
[解答群]
ア √3 cm² イ 2√3 cm² ウ 3√3 cm² エ 4√3 cm² オ 5√3 cm²
[問題2] 正四角すいの体積を求めなさい。
[解答群]
ア 28√6/3 cm³ イ 28√3/3 cm³ ウ 32√2/3 cm³ エ 32√3/3 cm³ オ 34√6/3 cm³
[問題3] 辺OA上にOP=1cmとなる点Pをとるとき、三角すいPABDの体積は正四角すいOABCDの体積の何倍ですか。
[解答群]
ア 1/8 倍 イ 1/4 倍 ウ 1/3 倍 エ 3/8 倍 オ 3/4 倍
解答と解説
試験問題1の解答:エ
三角形OADは、一辺が4㎝の正三角形です。一辺の長さをaとした場合の正三角形の面積を求める公式は次の通りです。
面積=(√3/4)a²
この公式を使わずに解くには、三平方の定理を知っている必要があります。上記の正三角形の面積を求める公式を覚えておいた方が、より短時間で解答することができますが、三平方の定理を使う問題は頻繁に出題されるので、どちらか一方しか覚える余裕がないという人は、三平方の定理を覚えておくようにしましょう。
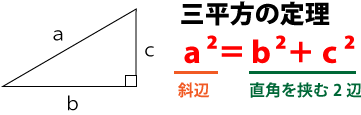
△OADの頂点Oから線分ADに垂線を下してその交点をQとすると、△OAQと△ODQの直角三角形が2つできます。△OADの頂点Oから線分ADに下した垂線OQが△OADの高さになります。垂線OQの長さは三平方の定理より、次の通り。
a²=b²+c²
OA²=QA²+OQ²
4²=2²+OQ²
16=4+OQ²
OQ²=12
OQ=2√3
よって、△OADの面積は次の通り
面積=4×2√3÷2
=4√3 cm²
試験問題2の解答:ウ
四角すいの体積を求める公式は覚える必要があります。
四角錘の体積=a²h/3
a:底面の一辺の長さ
h:四角錘の高さ
覚えにくいという人は次の形だと覚えやすいかもしれません。
四角錘の体積=底面積x高さ÷3
「底面積x高さ」だけだと一般的には四角形や円柱の体積になります。ただ、角錐の場合、四角形や円柱と違い先がとがっている分だけ体積が減ります。その減る分が1/3ということです。これは四角錘だけではなく三角錐や円錐も同様です。よって、下記の形で公式を覚えておけばあらゆる錐の体積を求めるのに使えます。
錘の体積=底面積x高さ÷3
今回の場合、一辺が4㎝の四角錘なので、底面積は次の通りです。
底面積=4×4=16
ここで問題になるのが、四角錘の高さです。四角錘の高さは点Oから四角形ABCDの面に垂直に下した垂線ORが高さとなります。
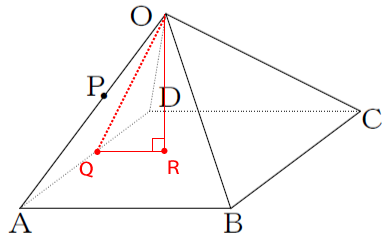
ここで再び三平方の定理を使用します。OQの長さは問題1の中で既に求めています。QRの長さは一辺の長さの半分なので2だとわかります。
OQ²=QR²+OR²
(2√3)²=2²+OR²
OR²=12-4
OR=2√2
よって、四角錘の体積は次の通り。
四角錘の体積=底面積x高さ÷3
=16×2√2÷3
=32√2/3
試験問題3の解答:エ
これまでと同様に「三平方の定理」と「錐の体積の公式」を覚えていれば解くことができます。
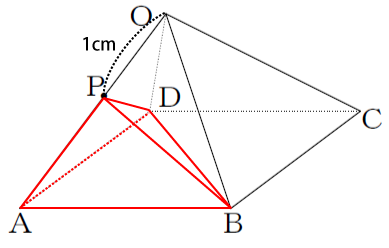
底面となる三角形ABDの面積は正四角形ABCDの半分なので次の通りになります。
△ABD面積=4×4÷2=8
三角錐PABDの高さは点Pから三角形ABDに下した垂線PSです。ここで、気が付いて欲しい点は、三角形OARと三角形PASは相似な三角形だという点です。
線分OA:PA=4:3
よって、三角錐の高さPSも同様に次の通りになります。
OR:PS=4:3
線分ORの長さは問題2のときに「2√2」と分かっているので、線分PSは次の通りになります。
線分PS=(2√2)x(3/4)
=3√2/2
よって、三角錐の体積は次の通り。
三角錐の体積=8x(3√2/2)÷3
=4√2
正四角錘の体積は問題2より、32√2/3だと分かっているので、求めたい倍率をMとした場合、倍率は次の通り。
(32√2/3)xM=4√2
M=(4√2)x(3/32√2)
=3/8
※解説を記載するまでもないと判断した問題に関しては、解説を記載せず解答のみを記載しています。もし、この問題の解説が欲しいというのがあれば、コメント欄に記載してください。また、記載している解説の内容も不明であれば遠慮なくコメントください。

