問1~2、問4に関しては以下のページに解説をまとめているので参考にして下さい。
図のようにすべての辺の長さが6cmの正四角すいOABCDがある。以下の問いにア~オから選 んで答えなさい。
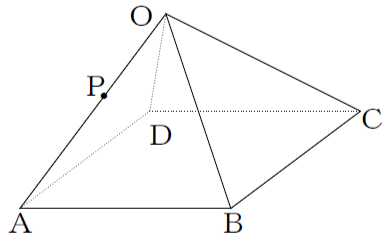
[問題1] △OABの面積を求めなさい。
[解答群]
ア √3 cm² イ 3√3 cm² ウ 5√3 cm² エ 7√3 cm² オ 9√3 cm²
[問題2] 正四角すいの体積を求めなさい。
[解答群]
ア 12√2 cm² イ 24√3 cm² ウ 36√2 cm² エ 48√3 cm² オ 60√2 cm²
[問題3] 辺OA上にOP=2cmとなる点Pをとるとき、三角すいPABDの体積を求めなさい。
[解答群]
ア 12√2 cm³ イ 24√3 cm³ ウ 36√2 cm³ エ 48√3 cm³ オ 60√2 cm³
解答と解説
試験問題1の解答:オ
この問題を解くには、以下のいずれかを知っておく必要があります。
- 正三角形の面積を求める公式
- 三平方の定理
できれば、「2.三平方の定理」の方を覚えておく方が他の問題でも応用できる場面が多いです。ここでは両方の解き方で解説します。
■正三角形の面積を求める公式を使って解く
正三角形の面積=(√3/4)a²
一辺の長さが6㎝なのでa=6
よって、三角形OABの面積は次の通り。
△OAB面積=(√3/4)x6²
=9√3 ㎝²
■三平方の定理を使って解く
頂点Oから辺ABに垂線を下し、その交点をQとします。
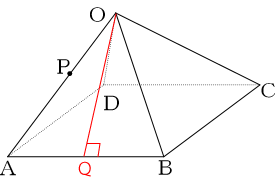
辺AQは、辺ABの半分なので長さは3㎝だと分かります。更に辺OAは6㎝なので、三平方の定理より、辺OQの長さは次の通りになります。
三平方の定理
a²=b²+c²
OA²=AQ²+OQ²
6²=3²+OQ²
OQ²=36-9=27
OQ=√27
=3√3
辺OQは三角形OABの高さになるので、三角形OABの面積は次の通り。
△OAB面積=6x(3√3)÷2
=9√3 ㎝²
試験問題2の解答:ウ
四角錘の体積を求める公式は次の通り。
四角錘の体積=底面積x高さ÷3
底面積
底面となる四角形ABCDは一辺が6㎝の正四角形なので面積は次の通り。
底面積=6×6=36㎝²
高さ
点Oから底面ABCDに垂線を下して交点となる点を点Rとします。
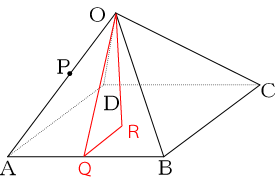
辺OQは、問題1より3√3だと分かっています。更に辺QRは、3㎝なので辺ORは三平方の定理より次のようになります。
三平方の定理
a²=b²+c²
OQ²=QR²+OR²
(3√3)²=3²+OR²
27=9+OR²
OR²=18
OR=√18
=3√2
よって、四角錘の体積は公式より次の通りになります。
四角錘の体積=底面積x高さ÷3
=36×3√2÷3
=36√2 ㎝³
試験問題3の解答:ア
三角錐の体積の公式も四角錘と同じです。
三角錐の体積=底面積x高さ÷3
よって、体積を求めるには底面積と高さを求める必要があります。
底面積
底面となる三角形ABDは直角二等辺三角形なので面積は次の通りです。
三角形ABDの面積=6×6÷2=18
高さ
点Pから三角形ABDに垂線を下し交点を点Sとします。この辺PSが三角錐PABDの高さとなります。三角形OARと三角形PASは3つの内角が等しいので相似な三角形になります。辺OPが2㎝ということは、辺PAは4㎝ということになります。
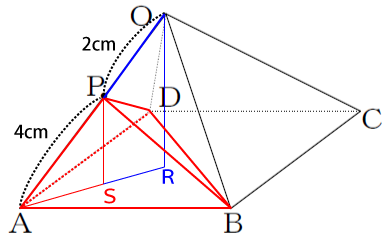
よって、辺OAと辺PAは次の式が成り立ちます。
OA:PA=6:4
よって、これにより次のことも言えます。
OR:PS=6:4
PS=(2/3)OR
ORの長さは、問題2より3√2だとわかっています。よって、PSの長さは次の通り。
PS=(2/3)x3√2
=2√2
よって、三角錐PABDの体積は次の通り。
三角錐の体積=18×2√2÷3
=12√2 cm³
※解説を記載するまでもないと判断した問題に関しては、解説を記載せず解答のみを記載しています。もし、この問題の解説が欲しいというのがあれば、コメント欄に記載してください。また、記載している解説の内容も不明であれば遠慮なくコメントください。

