問1~3に関しては以下のページに解説をまとめているので参考にして下さい。
大阪 職業訓練 短期過程試験問題 数学-問1
大阪 職業訓練 短期過程試験問題 数学-問2
大阪 職業訓練 短期過程試験問題 数学-問3
図は、y=x²のグラフと、点A(-1,1)と点B(2,4)を通る直線をℓとするとき、以下の問いにア~オから選んで答えなさい。
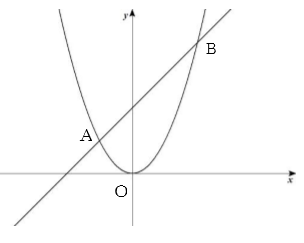
[問題1] 直線ℓの式を求めなさい。
[解答群]
ア y=x+1 イ y=x+2 ウ y=2x+1 エ y=2x+2 オ y=3x+2
[問題2] 点Oを通り、△OABの面積を二等分する直線mの式を求めなさい。
[解答群]
ア y=x イ y=2x ウ y=3x エ y=4x オ y=5x
[問題3] 直線ℓとy軸の交点をDとする。このとき△OBDをy軸を回転の軸として回転させるとき、できた立体の体積を求めなさい。
[解答群]
ア 5π/3 イ 8π/3 ウ 11π/3 エ 14π/3 オ 16π/3
解答と解説
試験問題1の解答:イ
直線ℓの傾きをa、y軸との交点である切片をbとした場合、次の式が成り立ちます。
y=ax+b
この式に点A(-1,1)と点B(2,4)の値を代入すると傾きa、切片bが求まり、直線ℓの式ができあがります。
点A(-1,1)を代入
y=ax+b
1=-x+b ・・・(1)
点B(2,4)を代入
y=ax+b
4=2x+b ・・・(2)
式(1)-式(2)を行います。
1=-a+b ・・・(1)
4=2a+b ・・・(2)
——————–
-3=-3a
a=1
直線ℓの傾きは1だと分かりました。更にa=1を式(1)もしくは式(2)に代入するとbの値も求まります。
1=-a+b ・・・(1)
1=-1+b
b=2
よって、直線ℓの式は次の通り。
y=x+2
試験問題2の解答:オ
三角形は、3つの頂点のいずれかの頂点からその対辺である辺の中点に線を引いて二等分すると面積も二等分される。これはどんな三角形でも言えることなので覚えておきましょう。
三角形の頂点Oから対辺である線分ABの中点に線を引き、三角形を二等分すると面積も二等分される。よって、まずは線分ABの中点を求める。
点Aの座標(-1,1)
点Bの座標(2,4)
点A、点BのX座標の中点は次の通り。
(-1+2)÷2=1/2
点A、点BのY座標の中点は次の通り。
(1+4))÷2=5/2
中点の座標(1/2,5/2)
求めたい直線mの傾きをaとした場合、直線の式は次の通り。
y=ax
この直線は線分ABの中点を通ることから、上記の式に中点の座標であるx=1/2、y=5/2を代入すると傾きaが求まり、直線mの式が出てきます。
5/2=a/2
a=5
よって、直線mの式は次の通り。
y=5x
試験問題3の解答:イ
点Bからy軸に垂線を引き、交点をEとする。求めたい図形の体積は、△OBEをy軸を軸に回転させてできた図形の体積から、△DBEをy軸を軸に回転させてできた図形の体積を引けば求まります。
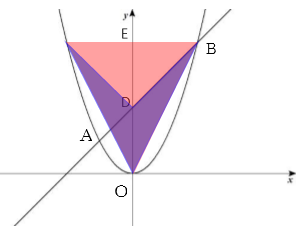
△OBEを回転させてできる体積
△OBEをy軸を軸に回転させると三角錐ができます。三角錐の体積を求める公式は次の通り。
三角錐体積=底面積x高さ÷3
底面積はEBを半径とする円の面積。EBの距離は点Bのx座標なので2。よって、底面積は次の通り。
底面積=2x2xπ
=4π
高さは点Eのy座標になるが、点Bのy座標と同じなので4だとわかります。よって、三角形OBEを回転させてできる三角錐の体積は次の通り。
三角錐体積=底面積x高さ÷3
=4πx4÷3
=16π/3 ・・・(1)
△DBEを回転させてできる体積
底面積は、既に求めた△OBEを回転させてできる三角錐の底面積と同じ。よって、底面積は、4π。
高さは、EDの距離になります。これは、点Eのy座標から点Dのy座標を引けば求まる。
EDの距離=点Eのy座標-点Dのy座標
=4-2
=2
———————–
※補足
点Dのy座標は、問題1で求めた直線ℓの式で簡単に分かる。直線の式「y=ax+b」のbはy軸との交点座標を表します。
直線ℓの式
y=x+2
よって、直線ℓのy座標は(0,2)となる。
————————
三角錐体積=底面積x高さ÷3
=4πx2÷3
=8π/3 ・・・(2)
よって、△OBDを回転させてできる三角錐の体積は次の通り。
求めたい三角錐の体積=式(1)-式(2)
=(16π/3)-(8π/3)
=8π/3
※解説を記載するまでもないと判断した問題に関しては、解説を記載せず解答のみを記載しています。もし、この問題の解説が欲しいというのがあれば、コメント欄に記載してください。また、記載している解説の内容も不明であれば遠慮なくコメントください。

