問1~2、問4に関しては以下のページに解説をまとめているので参考にして下さい。
大阪 職業訓練 短期過程試験問題 数学-問1
大阪 職業訓練 短期過程試験問題 数学-問2
大阪 職業訓練 短期過程試験問題 数学-問4
円すいについて、以下の問いにア~オから選んで答えなさい。円周率はπとします。
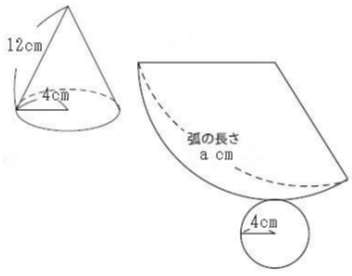
[問題1] 展開図のaの値を求めなさい。
[解答群]
ア 8π イ 16π ウ 12 エ 4π オ 12π
[問題2] 円すいの表面積を求めなさい。
[解答群]
ア 64cm² イ 48πcm² ウ 48cm² エ 16πcm² オ 64πcm²
[問題3] 円すいの体積を求めなさい。
[解答群]
ア 192πcm³ イ 64πcm³ ウ 96πcm³ エ (128√2)π/3 cm³ オ (64√2)π/3 cm³
解答と解説
試験問題1の解答:ア
弧aの長さは、底面の円の円周の長さに等しいので、円の円周を求めればよい。
弧aの長さ=円の直径xπ
=(4+4)xπ
=8π
試験問題2の解答:オ
円錐の表面積は、扇型の面積と底面の円の面積の合計になります。
円錐の表面積=扇型の面積+円の面積
円の面積を求める
底面の円は半径4cmの円なので面積は次の通り。
円の面積=4x4xπ
=16π
扇型の面積を求める
扇型は図のように半径12cmの円の一部になります。
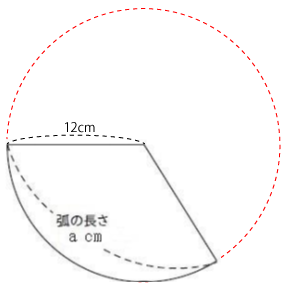
半径12cmの円の円周は次の通り。
(12+12)xπ=24π
扇型の弧の長さは問題1より、8πだとわかっています。このことより次のことが言えます。
8π÷24π=1/3
扇型は半径12cmの円を1/3にした大きさ。よって、面積も半径12cmの円の1/3になる。
円の面積=12x12xπ
=144π
よって、扇型の面積は次の通り
144π÷3=48π
円錐の面積を求める
円錐の表面積=扇型の面積+円の面積
=16π+48π
=64π cm²
試験問題3の解答:エ
円錐の体積を求める公式は次の通り。
円錐の体積=底面積x高さ÷3
底面積は問題2で既に求めているので、分かっていないのは円錐の高さ。円錐の高さは三平方の定理を使って求めることができる。
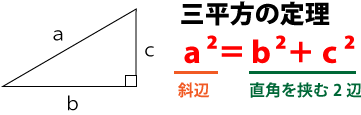
三平方の定理より円錐の高さは次の通り
12²=4²+c²
c²=144-16
c²=128
c=√128
=8√2
よって、円錐の体積は公式より次の通り。
円錐の体積=底面積x高さ÷3
=16πx8√2÷3
=128√2/3 cm³
※解説を記載するまでもないと判断した問題に関しては、解説を記載せず解答のみを記載しています。もし、この問題の解説が欲しいというのがあれば、コメント欄に記載してください。また、記載している解説の内容も不明であれば遠慮なくコメントください。

