この問題は平成30年10月入校（試験実施日：平成30年8月24日）の大阪職業訓練短期過程の選考試験問題問2の解説です。特に難しい問題はありませんが、間違いやすい問題もあるのでこれらの過去問を繰り返し実施し、短時間かつ正確に解けるようにしておきましょう。

実際の試験の問題用紙は以下のページで確認することができます。

⇒大阪府職業訓練校試験問題（平成30年度8月24日実施 短期課程

問1、問3～問4に関しては以下のページに解説をまとめているので参考にして下さい。

問２ 試験問題

次の文章題の答えとして正しいものをア～オの中から1つ選び、記号で答えなさい。

[問題1]　正八角形の1つの外角の大きさはいくらか。

[解答群]

  • 30
  • 45
  • 60
  • 108
  • 135

[問題2]　母と子の年齢は32才離れている。8年後に母の年齢は子の年齢の3倍になる。8年後の子の年齢を求めよ。

[解答群]

  • 8才
  • 12才
  • 16才
  • 20才
  • 24才

[問題3]　yがXに反比例し、X＝3のとき、y=-2である。X＝6のときのyの値はいくらか。

[解答群]

  • ｙ＝-1
  • ｙ＝-12
  • ｙ＝12
  • ｙ＝1
  • ｙ＝32

[問題4]　関数ｙ＝2X²のXの変域が-2＜X＜3であるとき、ｙの変域は0≦ｙ＜ａである。このときaの値を求めよ。

[解答群]

  • 2
  • 4
  • 8
  • 12
  • 18

[問題5]　1800にできるだけ小さい自然数を加えて、ある整数の2乗になるようにしたい。加える自然数の値を求めよ。

[解答群]

  • 36
  • 49
  • 64
  • 81
  • 100

解答と解説

解答と解説を記載していきます。
解き方が分からないという人を少しでも減らすためにできる限り分かり易く必要以上に細かく順を追って解説している部分がありますが、実際の試験時は丁寧に計算し過ぎると時間のロスに繋がるため、自分の分かるところは効率よく解答していくようにしてください。

■目次

  1. 問題１の解答と解説
  2. 問題２の解答と解説
  3. 問題３の解答と解説
  4. 問題４の解答と解説
  5. 問題５の解答と解説

問題１の解答と解説

試験問題１の解答：イ

この問題の解き方は以下の2通りあります。

解き方

  1. 正八角形の1つの内角を求めそこから外角を求める方法
  2. 多角形の外角の総和から求める方法

いずれの方法にせよまず、外角が何なのかという点を知らないと解くことができません。

外角とは、下図のような三角形ABCがあった場合、∠ACBの外角は辺BCを延長してできる点をDとすると∠ACDが外角となります。そして、その角度は180°－∠ACBとなります。

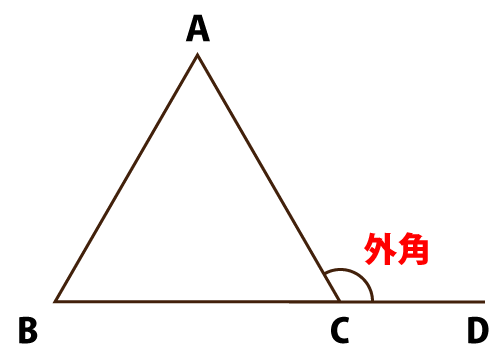
三角形の外角

よって、三角形の内角∠ACBが分かれば外角ACDが求まります。これが1つ目の解き方になります。

しかし、時間をかけずに解くには解き方２の『多角形の外角の総和から求める方法』の方法を知っている必要があります。実は多角形の外角の総和は360°となります。これはどんな多角形でも言えることです。

多角形の外角の総和＝360°

よって、正八角形の外角の総和も360°なので、1つの外角は次の通りになります。

360÷8＝45°

問題２の解答と解説

試験問題２の解答：ウ

求めたい子供の年齢をＮと仮定すると母の年齢は次の通りになります。

子供の年齢：Ｎ
母親の年齢：Ｎ+32

そうすると、8年後の子供と母親の年齢は次の通りになります。

子供の年齢：Ｎ+8
母親の年齢：Ｎ+40

問題文より、8年後に母の年齢は子の年齢の3倍になるということなので以下の式が成り立ちます。

(Ｎ+8)×3＝(Ｎ+40)

この式を解くと求めたい子供の年齢がでてきます。

(Ｎ+8)×3＝(Ｎ+40)
3Ｎ+24＝Ｎ+40
2Ｎ＝16
Ｎ＝8

ここで間違えてはダメなのが設問は8年後の子供の年齢です。Ｎは現在の年齢なので、8年後の子供の年齢は次の通りになります。

8年後子供の年齢＝8+8＝16才

問題３の解答と解説

試験問題３の解答：ア

ｙがXに比例する場合は、『ｙ＝ax』の式が成り立つのですが、今回の問題は反比例です。

反比例の場合は以下の式が成り立ちます。これは覚えておいてください。

ｙ＝ａX

問題文よりX＝3のとき、ｙ＝-2ということなので上の式に代入し、係数ａの値を求めます。

ｙ＝ａX
-2＝ａ3
ａ＝-6

よって、反比例の式は次の通りになります。

ｙ＝-6X

そして、X＝6のときのｙの値は次のようになります。

ｙ＝-6X
　＝-66
　＝-1

問題４の解答と解説

試験問題４の解答：オ

ｙ＝2ｘ²は、頂点が原点で上向きのグラフだと瞬時に頭に浮かぶようにしておきたいところです。

よって、原点からより離れたＸ座標の方がｙの値も大きくなります。したがって、今回の問題であればＸの値が-2のときよりも3のときの方が原点から離れた位置にあり、その時のｙ座標の値も大きくなることが頭の中だけで推測できます。

放物線

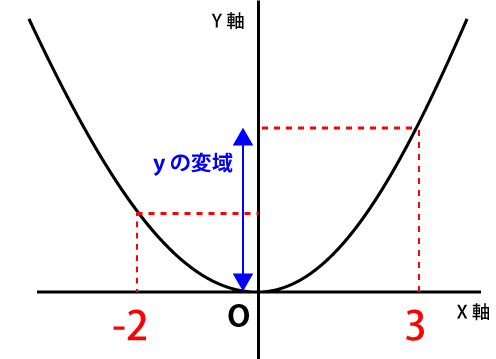
よって、Ｘ＝3のとき、ｙの値は次の通り。

ｙ＝2X²
　＝2×3²
　＝18

よって、ｙの変域は0≦ｙ＜18となります。

問題５の解答と解説

試験問題５の解答：イ

正しい解き方はあるもののはっきり言って力技で解いた方が早いです。

加える自然数をＮ
ある整数をＭ

と仮定した場合、以下の式が成り立ちます。

Ｍ²＝1800+Ｎ

そうすると求めたい加える自然数の値は次の式で表すことができます。

Ｎ＝Ｍ²-1800

求めたい自然数Ｎは自然数なので正の値であり、解答群ア～オのいずれかになります。よって、Ｍ²の値は1800より大きくなる必要があります。

すぐに求めることはできませんが、2乗して1800に近い値になるのは40だということはすぐわかりますよね？しかし、40の2乗は1600でＮの値がマイナスになってしまいます。よって、次に41、42と順に確認していきます。

そうすると、「41×41＝1681」、「42×42＝1764」、「43×43＝1849」となり、Ｍ＝43で1800を超えました。超えた数は49です。これを解答群から探すとありますよね？もしなければ続けて44,45と計算していきます。

少し強引なやり方ですが、この方が確実だと思います。

※解説を記載するまでもないと判断した問題に関しては、解説を記載せず解答のみを記載しています。もし、この問題の解説が欲しいというのがあれば、コメント欄に記載してください。また、記載している解説の内容に誤りや不明な点があれば遠慮なくコメントください。