次の(1)~(4)の問いに答えなさい。
[問題1]
長さ6mの針金で、縦と横の長さの比が7:8になるような長方形を作ると、縦の長さを求めなさい。
[問題2]
赤玉3個と白玉2個が入っている袋の中から、球を同時に2個取り出すとき、2個とも同じ色である確率を求めなさい。
[問題3]
16個入りのりんご1箱の代金が1325円で、そのうち箱の値段は45円であった。リンゴ1個の金額を求めなさい。
[問題4]
博物館の入館料は、大人500円、子供200円である。4月1日に300人が入館した。翌2日、大人の入館者数が前日と比べ10%増え、子供の入館者数が20%減った。翌2日の入館料が87,000円のとき、翌2日の大人の入館者数を求めなさい。
解答と解説
試験問題1の解答:
長さ6mの針金で長方形を作るので、長方形の4辺の合計は、6mになるのは当然ですね。また、縦1辺の長さと、横1辺の長さの合計は、その半分の3mとなります。
縦1辺の長さ:横1辺の長さ = 7 : 8
となる長さを求めたいので、縦1辺の長さと、横1辺の長さの合計3mを7:8に分ければいい。真面目に比率計算で求めてもいいがこういった試験はいかに早く解くかが重要なので、できる限り簡潔にときたい。
7 : 8
というのは、全15の内の7と、8ということはわかるでしょうか? 例えば、下記の5つの□を3:2に分けて欲しいと言われれば、3つと2つに簡単に分けることができますよね。ようは、3:2というのは、全5つの内の3つと2つだと思ってもらってよい。
□ □ □ □ □
話を戻すと、求めたい縦の長さは、全15の内の7とわかるので、長さ3mを7/15すればよいことになる。
3 × 7/15 = 7/5 = 1.4
解答:1.4m
試験問題2の解答:
確率を求めたい場合は、下記の式を意識する様にしてほしい。確率を求めるときは、全パターン数と、求めたい対象のパターン数を出す必要がある。
今回の問題で言うと、全パターン数と言うのは、「赤玉3個と白玉2個の計5個から2個を選ぶ組合せ数」のことに該当する。また、求めたい対象のパターン数というのは、「同じ色の球を2個取り出す組み合わせ数」に該当する。

さらに、組み合わせ数を求めるには次の公式を知っておく必要がある。

それでは、まず、「赤玉3個と白玉2個の計5個から2個を選ぶ組合せ数」をもとめます。計5個から2個を選ぶので上記公式にあてはめると、次のようになります。
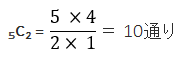
これで、確率を求める為の分母「全パターン数」がでました。次に、分子になる求めたい対象のパターン数を算出します。
同じ色を2個取り出すというのは、赤色から2個取り出す場合と、白玉から2個取り出す場合がある。この2つの場合を考えなければならない。まず、赤玉3個から2個を取り出す組み合わせ数は、先ほどと同様に公式にあてはめると次のようになる。
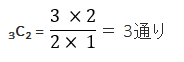
次に、白玉2個から2個を取り出す組合せですが、これは白玉は全部で2個しかないので組み合わせは1組しか存在しない。よって、「赤玉3個から2個を取り出す組み合わせ数」と「白玉2個から2個を取り出す組合」は、次の通り。
3 + 1 = 4
よって、分子になる求めたい対象のパターン数は、4となる。これを確率の式にあてはめると
求めたい確率 = 4 ÷ 10 = 2/5
解答:2/5
試験問題3の解答:
代金1,325円から箱代の45円を引く。
1325-45=1280
これが箱代を除いた代金なので、純粋にりんご代の合計となる。よって、りんごの個数16個で割るとりんご1個あたりの値段がわかる。
1280÷16=80円
解答:80円
試験問題4の解答:
4月1日の大人の人数を、N人とすると下記のことが言えます。
4月1日の大人の人数:N 人
4月1日の子供の人数:300-N 人
4月1日の入館者数:300 人
4月2日の大人の人数:1.1N 人
4月2日の子供の人数:0.8(300-N) 人
4月2日の入館者数:1.1N+0.8(300-N)=0.3N+240 人
4月2日の入館料が87,000円ということなので次の式がなりたちます。
1.1N × 500 + 0.8(300-N) × 200 = 87000
この式を解くと、4月1日の大人の人数がでてきます。
1.1N × 500 + 0.8(300-N) × 200 = 87000
550N + 160(300-N) = 87000
550N + 48000 -160N = 87000
390N = 39000
N= 100
4月1日の大人の人数は、100人。しかし、求めたいのは、4月2日の大人の人数なので、
4月2日の大人の人数 = 1.1N = 1.1 × 100 = 110人
よって、求める解答は、110人
解答:110人

