次の問いに答えなさい。
[問題1]
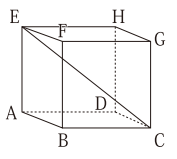
下の図のような、AB=2cm、BC=4cm、AE=4cmの直方体がある。対角線ECの長さを求めなさい。
解答と解説
試験問題1の解答:
この問題は、直角三角形の各辺の長さをもとめるための三平方の定理を知っていれば全く難しい問題ではない。三平方の定理は次の通り。
三平方の定理
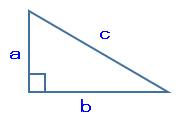
次の式が成り立つ
c² = a² + b²
解き方としては、まずは、辺ABと編BCが分かっているので三角形ABCとし、斜面ACを求める。このさいもこの三角形ABCは、直角三角形なので三平方の定理が使用できる。
続いて、辺AEと辺ACの長さが分かっているので、三角形ACEの斜面ECを求めればよい。これも三平方の定理を使用する。では、実際に計算を行ってみます。
AC²=AB²+BC²
AC²=2²+4²=4+16=20
ここで、AC²の2乗を解いてルート20としてもよいが、次の三角形ACEの斜面を求めるさいもAC²は使うので、AC²=20 のままにしておく方が賢い。
それでは、次に三角形ACEの斜辺ECを求めます。
EC²=AE²+AC²=4²+20=16+20=36
よって、
EC=6cm
解答:6cm

