(8)次の図のxの角度を求めなさい。
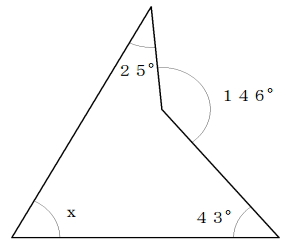
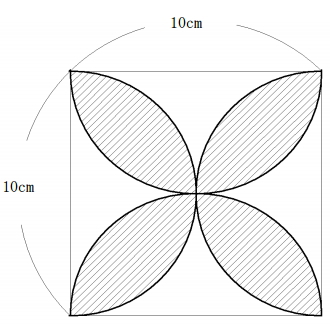
(9)次の図の斜線部分の面積を求めなさい。ただし、円周率はπとする。
解答と解説
問題1の解答&解説:
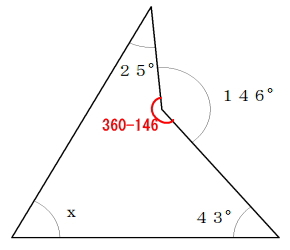
四角形の4角の内2角は25度、43度と既に分かっています。残り2角の内の1角も360度-146度=214度とすぐに分かります。
四角形の内角のは和は、360度なので360度から分かっている3角の角度を引けばXの角度を求めることができます。
X=360-25-43-214=78
よって、Xの角度は、78°
78°
問題2の解答&解説:
下図の様に図を4分割し、4分割した内の1つの面積を求め、最後に4倍すれば楽に求めることができます。今回は、①の部分に焦点を合わし面積を求めたいと思います。
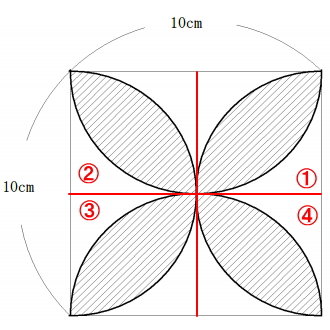
①の部分を抜き出すと下図の様になります。
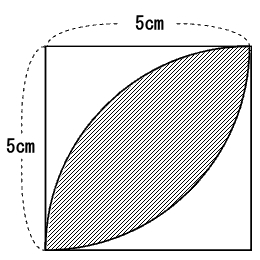
上図をよく見ると下図の様に半径5cmの扇形が重なり合ってできていることに気付きます。上図の斜線部分の面積は、下図のオレンジ部分の面積を2倍した値になります。よって、まずは、下図のオレンジ部分の面積を求めればよい。
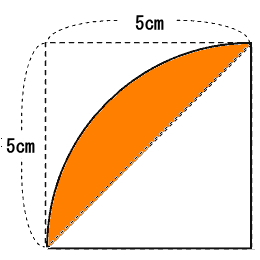
オレンジ部分の面積の求め方は、扇の面積を求めた後、三角形の面積を引けばいい。
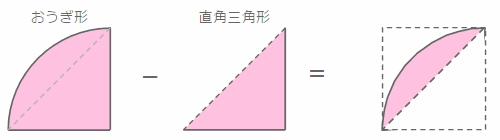
扇の面積は、半径5cmの円の面積を求めそれを4分の1にしたもの。
半径5cmの円の面積
円の面積=半径×半径×Π
=5×5×Π
=25Π
扇の面積
扇の面積=円の面積÷4
=25Π/4
三角形の面積
三角形の面積=底辺×高さ÷2
=5×5÷2
=25/2
オレンジ部分の面積
オレンジ部分の面積=扇の面積-三角形の面積
=(25Π/4)-(25/2)
①の斜線部分の面積
①の斜線部分の面積は、オレンジ部分の面積の2倍なので
①の斜線部分の面積={(25Π/4)-(25/2)}×2
=(25Π/2)-25
これで①の斜線部分の面積が求まりました。最初に4分割しているので、この①の斜線部分の面積を4倍すると、元の図形の黒斜線部分の面積を求めることができます。
元の図形の黒斜線部分の面積={(25Π/2)-25}×4
=50Π-100
よって、求める面積は、50Π-100 cm²
50Π-100 cm²

