次の問いに答えなさい。
[問題1]
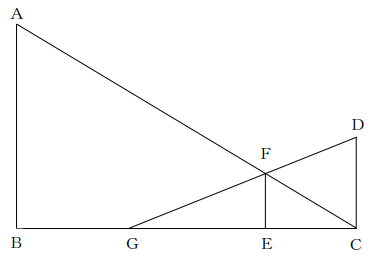
下の図のように、AB、FE、DCが平行であり、AB=9㎝、DC=4㎝、BG=5㎝、BC=15㎝のとき、FEの長さを求めなさい。
解答と解説
試験問題1の解答:
少しややこしいので頑張って理解してください。
まず、最初に三角形ABCにだけ着目します。ABと平行な線HGを引きます。そうすると、三角形ABCと、三角形HGCは、大きさが違うだけの相似三角形になります。よって、比率によりHGの長さを求めることができます。
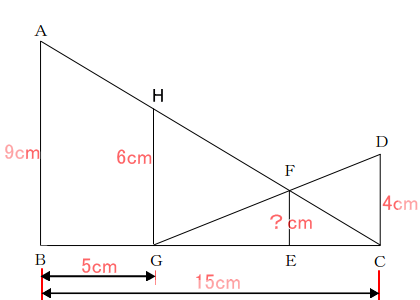
CB:CG=AB:HG
15:10=9:HG
15HG=90
HG=6cm
次に着目する三角形を変えます。三角形FHGと三角形FCDに着目します。HG、DCは並行なので、この2つの三角形もまた、大きさが違うだけの類似三角形になります。その比率は次の通り。
HG:DC = 6:4 = 3:2
よって、FGとFDの比率も同様に3:2となる。
FG:FD = 3:2
次に着目する三角形を三角形CDGと、三角形EFGに変えます。FEとDCは並行なので、この2つの三角形もまた、大きさが違うだけの類似三角形になります。では、この2つの三角形の比率はどうなのか? 先程、FG:FD = 3:2 と分かったので、小さい方の三角形EFGの斜辺FGが3に対して、大きい方の三角形CDGの斜辺DGは、5(=3+2)となります。
よって、この2つの三角形の大きさの比率は、3:5 だと分かります。そうすると、FEとDCの比率も3:5になるので、FEの長さを求めることができます。
FE:DC = 3:5
FE:4 = 3:5
5FE = 12
FE = 2.4
よって、求めたいFEの長さは、2.4cmとなる。
解答:2.4cm


解説ありがとうございます。
解説で 類似三角形は相似三角形といいませんか?
途中の解説で
誤)HG=4cm 正)HG=6cm
堂前様
コメントありがとうございます。
解説を修正させて頂きました。