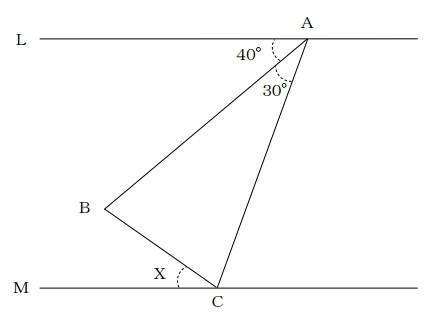
(9)次の図の長方形の色のついた部分の面積を求めなさい。
解答と解説
問題解答&解説:
解き方としては、四角形全体の面積を求めた後、中の白色部分を削除します。
四角形全体の面積=10×6=60cm² ・・・(1)
次に横長の白色部分の面積ですが、これは縦1cm、横10cmの長方形。よって白色部分の面積は、
横長白部分の面積=1×10=10cm² ・・・(2)
次に縦長の白色部分の面積ですが、これは高さ6cm、横2cmの平行四辺形。平行四辺形の面積を求める公式は、高さ×横。よって、縦長の白色部分の面積は、
縦長白部分の面積=6×2=12cm² ・・・(3)
よって、白色部分の面積の合計は(2)+(3)となるのですが、そのまま足してしまうと横長と縦長の白色部分がクロスしている部分(下図の赤で囲っている部分)が2重でカウントしてしまっていることになります。
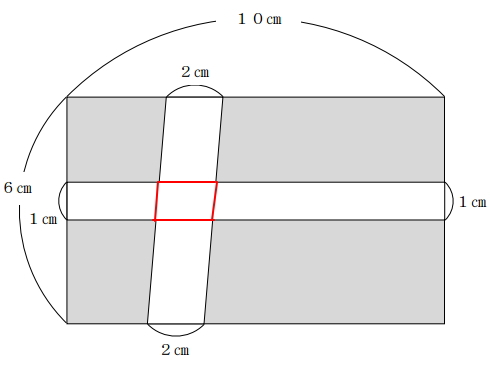
よって、この赤色で囲った部分の面積を引いてやる必要があります。赤色で囲った部分は、高さ1cm、よこ2cmの平行四辺形です。よって、その面積は、
赤色で囲った部分の面積=1×2=2cm² ・・・(4)
よって、白色部分の総面積は次の通りです。
白色部分の総面積=(2)+(3)-(4)
=10+12-2
=20cm²
これを、四角形全体の面積(1)から引くとグレー部分だけの面積がもとまります。
グレー部分の面積=60-20=40cm²
よって、求める解答は40cm²
40cm²

