埼玉職業訓練試験問題[短期] 数学-問3(平成27年入校生)

平成27年度に埼玉県で実施された職業訓練(短期コース)の選考試験で出題された試験問題と、その解答と解説です。本ページでは数学問題の問題3(正式なテスト用紙上では設問7)のみ記載しています。その他の問題に関しては、以下のページを参照してください。

７. 次の問いに答えなさい。

[問題1]
下の図の中に三角形はいくつあるか。

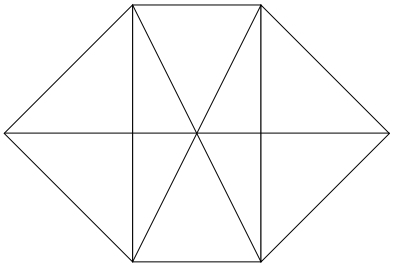
[問題2]
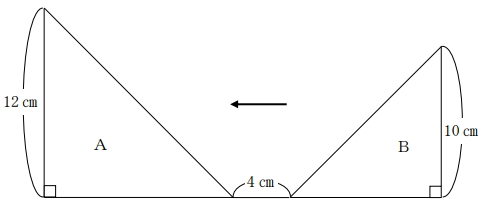
下の図のように４センチメートル離れて２つの直角二等辺三角形ＡとＢがある。Ａは動かさないで、Ｂを直線にそって左の方向に毎秒２センチメートルの速さで
動かす。このとき、動かし始めて４秒後に、２つの三角形が重なった部分の面積は何平方センチメートルか。

試験問題１の解答：
図から１つずつ数えていきましょう。

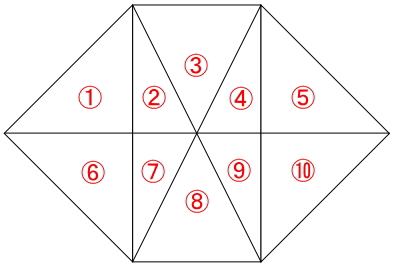
saitama-27-q3-t-3

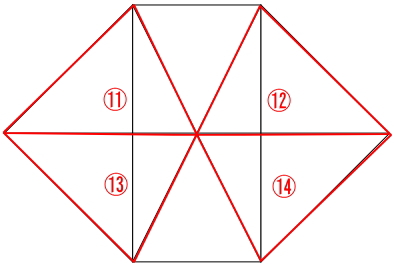
saitama-27-q3-t-4

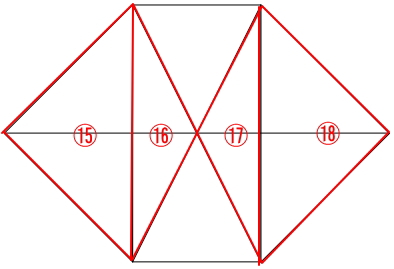
saitama-27-q3-t-5

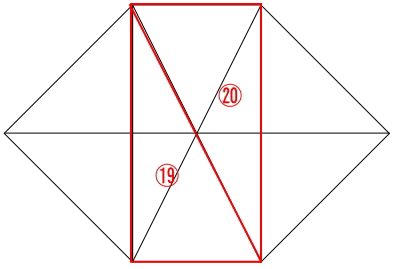
saitama-27-q3-t-6

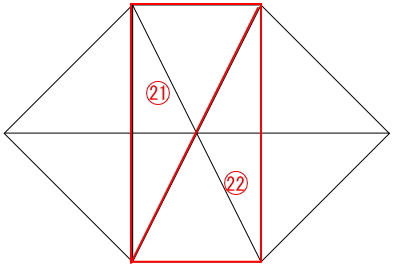
解答：２２

試験問題２の解答：
三角形Ｂは、1秒間に2cm左に動くので、4秒間で8cm動くことになります。元々から三角形Ａと三角形Ｂは4cmの隙間があったので、4秒間の移動で4cm重なる(8cm-4cm＝4cm)ということが分かります。図にすると下図の通り。

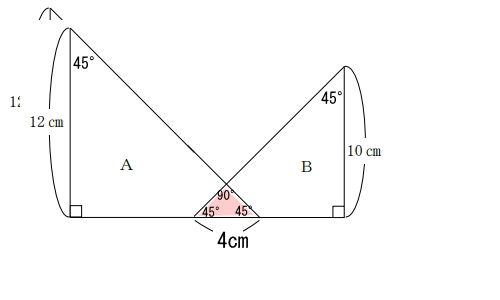
求めたいのは、色が付いた部分の三角形です。この問題を解く上で知っておかなければならない点は、2点。

三角形の面積を求める公式
面積＝底辺ｘ高さ÷２

三平方の定理
直角三角形の場合、各辺の長さは下図のように1：1：√2となります。

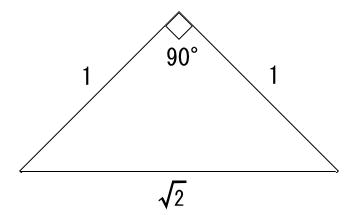
これを今回求めたい直角三角形にあてはめると下図のようになります。

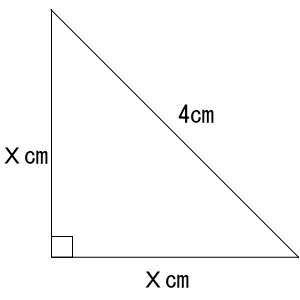
Ｘの長さが分かればこの三角形の面積が求まります。三平方の定理よりＸの長さは次の通りになります。
1：√2＝Ｘ：4
Ｘ√2＝4
Ｘ＝4/√2

求めたい三角形の面積は次の通り。
面積＝底辺ｘ高さ÷2
　　＝(4/√2)x(4/√2)÷2
　　＝(16/2)÷2
　　＝4cm²

※補足

三角形の面積を求める公式は「底辺ｘ高さ÷２」ですが、直角二等辺三角形の場合は、直角になる角の対辺(今回であれば4cmとなる辺)のみが分かっていれば次の公式で面積を求めることができます。

面積＝(直角になる角の対辺の長さ)²/4

よって、今回の問題であれば面積は次の通りになります。
面積＝4²/4＝4cm²

解答：4cm²

“埼玉職業訓練試験問題[短期] 数学-問3(平成27年入校生)” への2件のフィードバック