埼玉職業訓練試験問題[短期] 数学-問4(平成27年入校生)

平成27年度に埼玉県で実施された職業訓練(短期コース)の選考試験で出題された試験問題と、その解答と解説です。本ページでは数学問題の問題4(正式なテスト用紙上では設問8)のみ記載しています。その他の問題に関しては、以下のページを参照してください。

８. 次の問いに答えなさい。

[問題1]
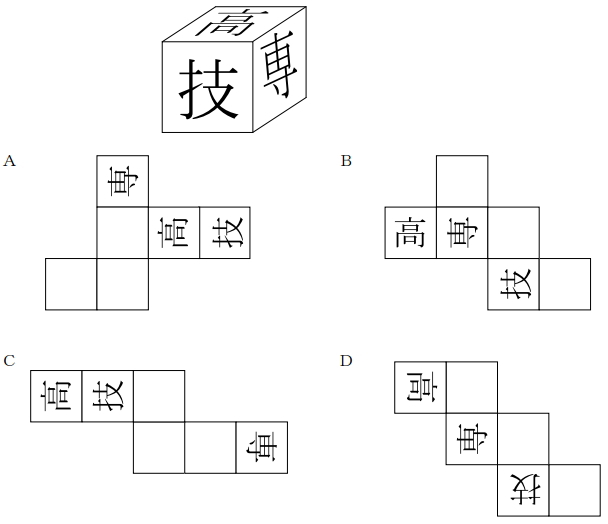
下の立方体の展開図として正しいものは次のうちどれか。記号で答えなさい。

[問題2]
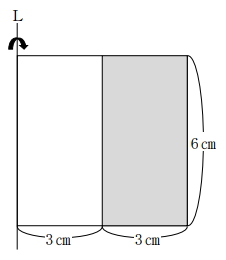
下の色のついた長方形を、直線Ｌを軸として１８０度回転させたときにできる立方体の体積はいくつか。ただし、円周率は３.１４とする。

試験問題１の解答：
立方体を展開するのではなく、展開された解答群の方を組み立てるようにしていきましょう。基本的には順番に組み立てて確認していくしかありません。

解答：Ｄ

試験問題２の解答：
実際に180°回転させた時にできる立方体は下図のようなかまぼこ状のものになります。求めたい体積は、真ん中の白色半円柱をくり抜いた灰色部分の半円柱の体積です。

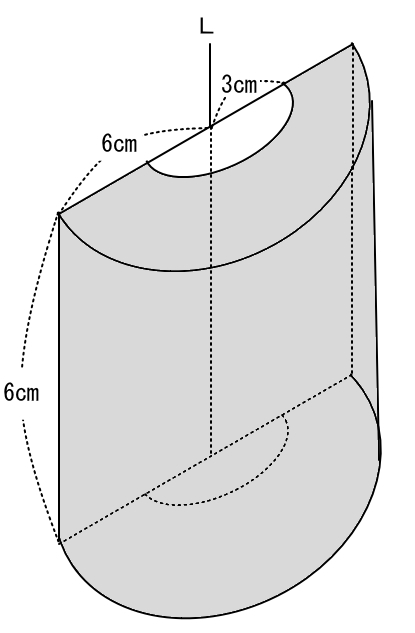
円柱の体積

求め方としては、次の流れで行います。

また、この問題を解くにあたり、知っておかなければならないのが円柱の体積を求める公式です。

円柱の体積＝底面積ｘ高さ

円柱の底面は円なので底面積を求めるには円の面積を求める公式も知っておかなければなりません。

円の面積＝半径x半径x3.14

半円柱全体の体積を求める
まずは、底面積を求める。底面は半径6cm(3cm+3cm)の円を半分にした半円なので以下の式で求まります。

底面積＝(半径x半径xπ)÷2
　　　＝(6x6xπ)÷2
　　　＝18π

円柱の面積は、底面積に高さを掛ける必要があるので半円柱全体の体積は次の通り。

半円柱全体の体積＝18πx6
　　　　　　　　＝108π ・・・(１)

※補足

円周率は3.14で計算する必要があるが、小数計算が入ると計算に時間がかかってしまうためπで計算し、最後の最後で3.14に置き換えると計算が楽になる。

内側の白半円柱の体積を求める
白半円柱の底面積を求める。底面は半径3cmの円を半分にした半円なので以下の式で求まります。

底面積＝(半径x半径xπ)÷2
　　　＝(3x3xπ)÷2
　　　＝4.5π

円柱の面積は、底面積に高さを掛ける必要があるので白半円柱の体積は次の通り。

半円柱全体の体積＝4.5πx6
　　　　　　　　＝27π ・・・(２)

半円柱全体の体積から内側の白半円柱の体積を引く
求めたい灰色部分の体積は(１)から(２)を引いた値になります。

体積＝108π-27π
　　＝81π
　　＝81×3.14
　　＝254.34cm³

解答：254.34cm³

“埼玉職業訓練試験問題[短期] 数学-問4(平成27年入校生)” への2件のフィードバック