平成28年度に埼玉県で実施された職業訓練の選考試験で出題された試験問題と、その解答と解説です。 本ページでは数学問題の設問3(正式なテスト用紙上では設問6)のみ記載しています。数学問題の設問1~2に関しては、以下のページを参照してください。
埼玉 職業訓練 試験問題[長期] 数学-問1(平成28年入校生)
埼玉 職業訓練 試験問題[長期] 数学-問2(平成28年入校生)
試験問題 設問3
下の図でAC、CD、BDの長さが同じであるとき、∠CAEの角度を求めなさい。
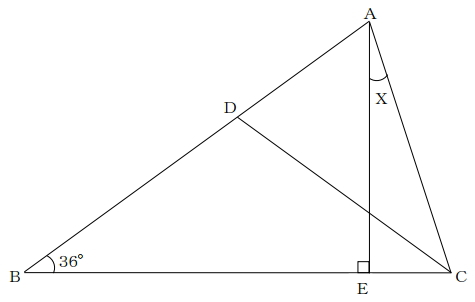
解答と解説
設問の内容からAC、CD、BDの長さが等しいことは分かっています。
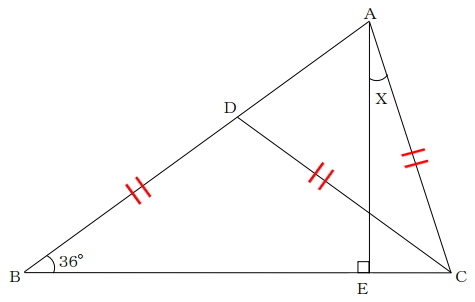
CDとBDの長さが等しいということは、三角形BCDは二等辺三角形ということになります。よって、∠DCBは36度というのがすぐに分かります。
∠DCB=36° ・・・(1)
三角形の内角の和は180°なので、∠BDCは次の通り。
∠BDC=180-36-36=108°
次に∠BDCが108°ということは∠ADCは次の通りになります。
∠ADC=180-108=72°
ACとCDの長さが等しいので、三角形ACDも二等辺三角形になります。よって、∠CADは、∠ADCと等しくなることが分かります。
∠CAD=72°
三角形の内角の和は180°なので、∠ACDは次のように求めることができます。
∠ACD=180-72-72=36°
∠DCBは(1)より、36°と分かっています。よって、∠ACEは次のように求めることができます。
∠ACE=∠ACD+∠DCB
=36°+36°=72°
∠CEAは90°なので、求めたいXは次の通りです。
X=180-72-90=18°
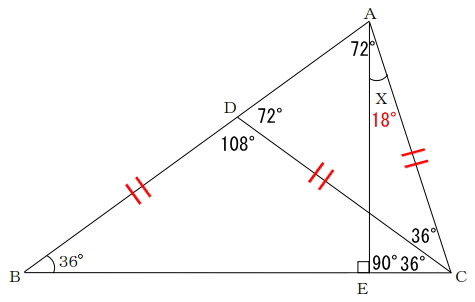
解答:18°

