平成29年度に埼玉県で実施された職業訓練の選考試験で出題された試験問題と、その解答と解説です。 本ページでは数学問題の設問3(正式なテスト用紙上では設問8)のみ記載しています。数学問題の設問1~2に関しては、以下のページを参照してください。
埼玉 職業訓練 試験問題[長期] 数学-問1(平成29年入校生)
埼玉 職業訓練 試験問題[長期] 数学-問2(平成29年入校生)
試験問題 設問3
下図のように、三角形ABCの辺AB上にAD=DE=EBを満たすように点D、Eをとります。辺BCの中点をFとし、点EとF、DとCをそれぞれ結び、線分AFとDCの交点をGとします。EF=9cmのとき、CGの長さは何cmか求めなさい。
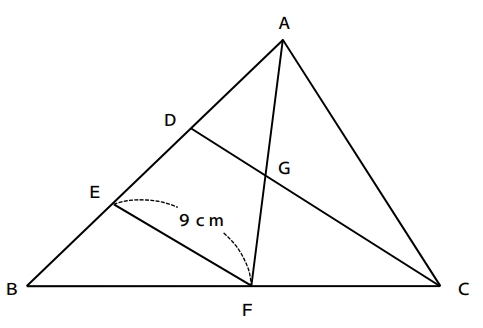
解答と解説
設問の内容を図に落とし込むと下図のようになります。
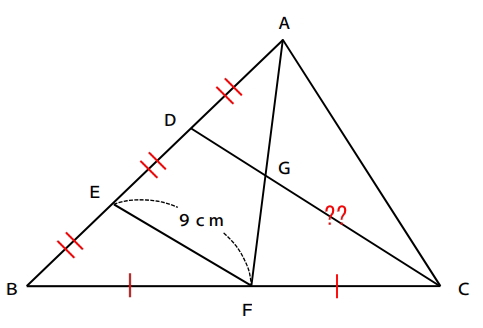
この問題を解くのに知っておく必要があるのが、三角形の相似条件です。
※三角形の相似条件
- 3組の辺の比が、すべて等しいとき
- 2組の辺の比とその間の角が、それぞれ等しいとき
- 2組の角が、それぞれ等しいとき
三角形BFEと三角形BCDについて考える
三角形BFEと三角形BCDは、下記の条件を満たしているので相似な三角形と言える。
- ∠Bは共通の頂点で角度が等しい
- 三角形BFEの辺BEと三角形BCDの辺BDの長さ比は1:2。
- 三角形BFEの辺BFと三角形BCDの辺BCの長さ比は1:2。
よって、三角形の相似条件「2組の辺の比とその間の角が、それぞれ等しいとき」を満たしているので三角形BFEと三角形BCDは相似な三角形。
相似な三角形の各辺の比率は同じになるため、三角形BFEの辺FEと三角形BCDの辺CDの長さ比も1:2となる。よって、辺FEの長さが9cmなので辺CDの長さは18cmになる。
三角形ADGと三角形AEFについて考える
三角形ADGと三角形AEFは、下記の条件を満たしているので相似な三角形と言える。
- ∠Aは共通の頂点で角度が等しい
- 三角形BFEと三角形BCDは前述の通り相似な三角形と分かっているので、∠FEB=∠CDBになる。これは、∠AEF=∠ADGを意味する。
よって、三角形の相似条件「2組の角が、それぞれ等しいとき」を満たしているので三角形ADGと三角形AEFは相似な三角形。
相似な三角形の各辺の比率は同じになる。三角形ADGの辺ADと三角形AEFの辺AEの長さ比は1:2です。よって、辺DGと辺EFの長さ比も1:2となるため、辺DGの長さは4.5cmとなる。
ここまでの結果を図に落とし込むと下図のようになります。
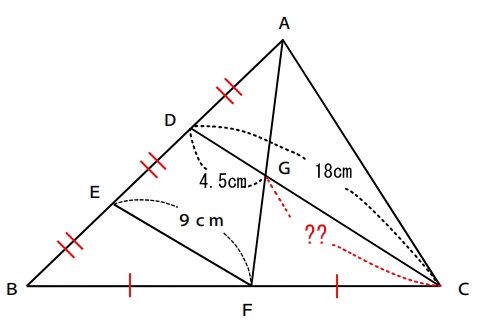
ここまでわかると、求めたい辺CGの長さはもうわかりますよね。
辺CGの長さ=18-4.5=13.5cm
解答:13.5cm

