この問題は平成25年4月入校の東京都立職業能力開発センター入校選考試験問題の問６の解答と解説です。

問１～問５に関しては以下のページに解説をまとめているので参考にして下さい。

実際の試験の問題用紙は以下のページで確認することができます。

⇒都立職業能力開発センター入校選考試験問題(平成25年04月生)

問題を解くのに必要な知識

  1. 特別な直角三角形の3辺の比
  2. 三平方の定理
  3. 余弦定理

※上記の1、2もしくは3のどちらかを知っていれば構いません。

問６ 試験問題

図のように、３地点Ａ、Ｂ、Ｃを結ぶ三角形の土地があります。ＡＢ＝８ｍ、ＢＣ＝５ｍ、∠ＡＢＣ＝60°のとき、ＡＣの長さは何ｍですか。

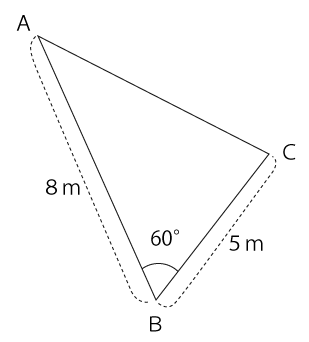
三角形の図

解答と解説

試験問題６の解答：7ｍ

△ABCの頂点Aから辺BCに垂線を引き、BCと交わる点をDとします。

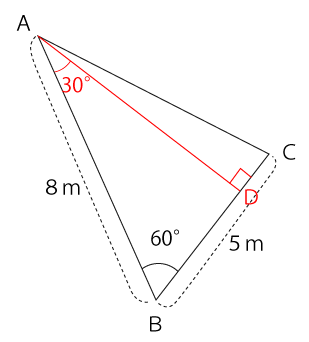
三角形の図

できた三角形ABDの∠BADは30°となります。
内角が30°、60°、90°となる三角形は特別な三角形で、以下のような各辺の比が成り立ちます。

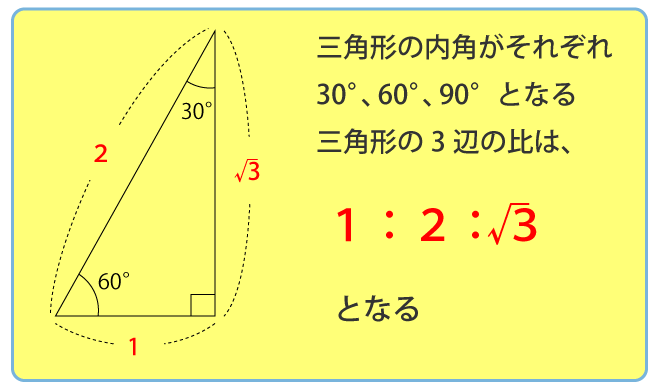
特別な三角形の比

よって、ABの長さが8ｍなのでADとBDの長さは次の通りになります。
AD＝4√3
BD＝4

BCは5ｍだと既にわかっているので、DCの長さも求まります。
DC＝5－4＝1

これでADの長さとDCの長さが分かったので三平方の定理を使用してACの長さを求めます。

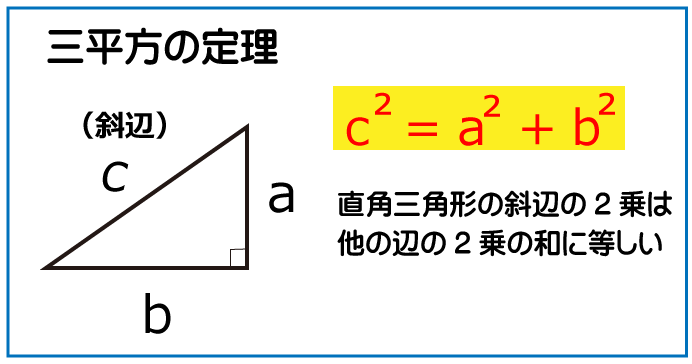
三平方の定理

AC²＝AD²＋DC²
AC²＝(4√3)²＋1²
　＝48＋1
　＝49
AC＝7

よって、求めたいACの長さは7ｍ

別の解き方

この問題は余弦定理を知っていれば簡単に解くことができます。

余弦定理

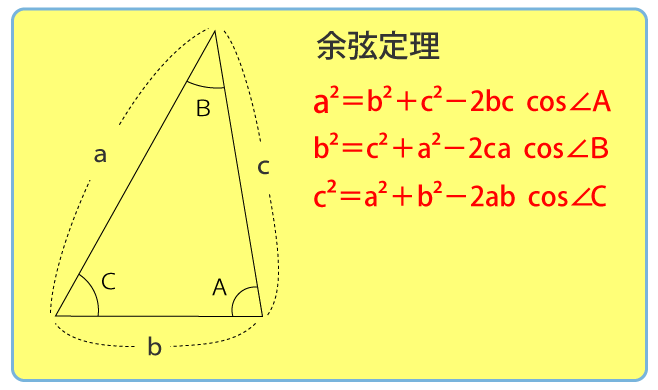
ｂ²＝ｃ²＋ａ²－2ｃａ cos∠Ｂ
AC²＝8²＋5²－2×8×5×cos60°
　＝64＋25－80×1/2
　＝64＋25－40
　＝49
AC＝√49
　＝7

よって、求めたいACの長さは7ｍ

※記載している解説の内容に誤りや不明な点があれば遠慮なくコメントください。