この問題は平成28年4月入校の東京都立職業能力開発センター入校選考試験問題の問５の解答と解説です。

問１～問４、問６に関しては以下のページに解説をまとめているので参考にして下さい。

実際の試験の問題用紙は以下のページで確認することができます。

⇒都立職業能力開発センター入校選考試験問題(平成28年04月生)

問題を解くのに必要な知識

  • 円柱の体積の求め方(公式)

問５ 試験問題

下図のように塗りつぶされた図形を、軸Ａを中心に回転したときにできる体積は何ｍ³ですか。

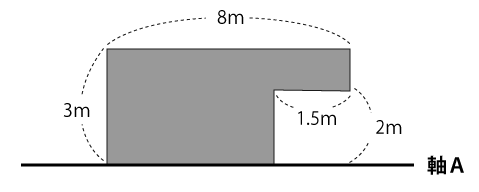
立体の回転と体積

以下は解答と解説です。解答、解説を見る前にまずは自分自身で解けるか試してみてください。

解答と解説

試験問題５の解答：66π ｍ³

この問題は円柱の体積の求め方を知っていれば簡単に解ける問題です。

円柱の体積＝底面積(円の面積)×高さ

図形を軸Ａを中心に回転させると下図のようになります。

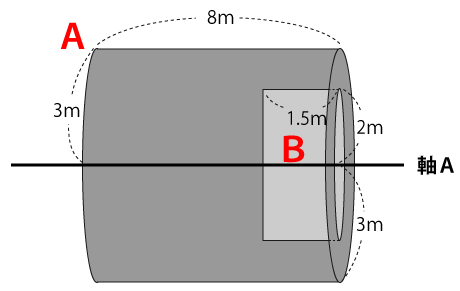
立体を回転させた図形

この立体の体積は次の流れで求めていきます。

  1. 円柱Ａの体積を求める
  2. 円柱Ｂの体積を求める
  3. 円柱Ａの体積から円柱Ｂの体積を引く

円柱Ａの体積を求める

立体の底面である円の半径は3㎝です。よって、この円の面積は次の通り。

底面積(円の面積)＝半径×半径×π
　　　　　　　　＝3×3×π
　　　　　　　　＝9π

円柱の体積＝底面積×高さ
　　　　　＝9π×8
　　　　　＝72π・・・①

円柱Ｂの体積を求める

小さい方の円柱Ｂの底面である円の半径は2ｍです。よって、この円の面積は次の通り。

底面積(円の面積)＝半径×半径×π
　　　　　　　　＝2×2×π
　　　　　　　　＝4π

円柱の体積＝底面積×高さ
　　　　　＝4π×1.5
　　　　　＝6π・・・②

求めたい立体の体積を求める

大きい円柱Ａの体積は①72π、小さい方の円柱Ｂの体積は②6πと分かったので、求めたい立体の体積は次の通り。

求めたい立体の体積＝①-②
　　　　　　　　　＝72π-6π
　　　　　　　　　＝66π

よって、図形を軸Ａを中心に回転したときにできる体積は66π ｍ³となります。

※記載している解説の内容に誤りや不明な点があれば遠慮なくコメントください。