この問題は平成28年1月入校の東京都立職業能力開発センター入校選考試験問題の問2の(1)と(2)の解答と解説です。
問1および、問2の(3)~(5)に関しては以下のページに解説をまとめているので参考にして下さい。
実際の試験の問題用紙は以下のページで確認することができます。
■目次
試験問題 問2(1)
赤、青、黄色の3本のテープがあります。赤色のテープの長さは2.5mです。青色のテープが赤色のテープの1.2倍、黄色のテープが6mのとき、黄色のテープは青色のテープの何倍ですか。
解答と解説
問2(1)の解答:2倍
問題を図式化すると下図のようになります。
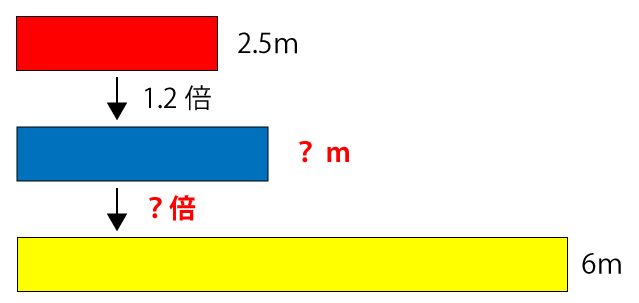
青色のテープは、赤色のテープの長さの1.2倍なので、その長さは次の通りになります。
青色のテープの長さ=2.5×1.2
=3m
黄色のテープの長さは6mなので、黄色のテープの長さは青色のテープの2倍になります。
試験問題 問2(2)
図のように2直線l、mが点Aで交わっています。直線lの式はy=2X+2です。また、直線mとX軸との交点をBとします。点AのX座標が1、点BのX座標が5のとき、直線mの式を求めなさい。

解答と解説
問2(2)の解答:y=-X+5
問題文から分かっている点を図に書き込むと下図のようになります。
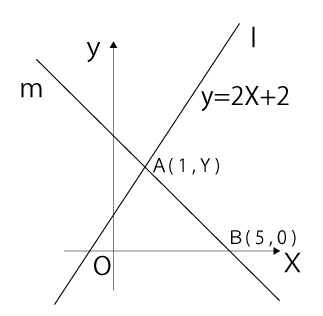
まずは、点Aのy座標を求めます。
点Aは直線l上の点なので、X=1を代入してyの値を求めます。
y=2X+2
y=2+2
=4
よって、点Aの座標は( 1 , 4 )
直線mの式をy=aX+bと仮定します。この直線は点A(1,4)と点B(5,0)の2点を通るので、直線の式に代入し、aとbを求め直線の式を完成させます。
点A(1,4)を通るので直線mの式は次のようになります。
y=aX+b
4=a+b・・・①
さらに点B(5,0)も通るので直線mの式は次のようになります。
y=aX+b
0=5a+b・・・②
式①-式②を行い傾きaを求めます。
4=a+b・・・①
0=5a+b・・・②
4-0=(a+b)-(5a+b)
4=-4a
a=-1
aの値を式①もしくは式②へ代入しbの値も求めます。ここでは式②に代入します。
0=5a+b・・・②
0=-5+b
b=5
よって、直線mの式は次の通り。
y=-X+5
※記載している解説の内容に誤りや不明な点があれば遠慮なくコメントください。

