この問題は平成29年7月入校の東京都立職業能力開発センター入校選考試験問題の問2の(5)の解答と解説です。
問1および、問2の(1)~(4)に関しては以下のページに解説をまとめているので参考にして下さい。
実際の試験の問題用紙は以下のページで確認することができます。
試験問題 問2(5)
図のような、底面の半径が4cm、母線の長さが12cmの円錐に内接する球の半径は何cmですか。
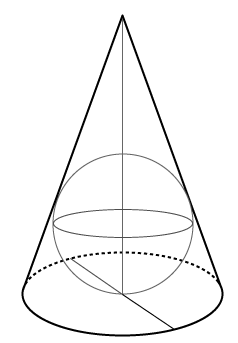
解答と解説
問2(5)の解答:2√2cm
この問題を解くには三平方の定理を知っている必要があります。
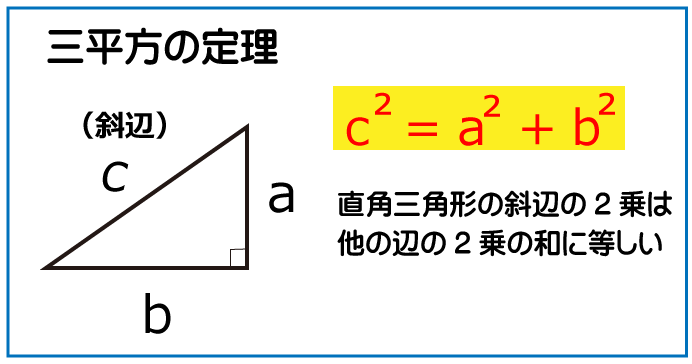
さらに円すいの母線についても知っている必要があります。
問題文には底面の半径が4cm、母線の長さが12cmの円すいと書かれていますが、図にはその長さが書き込まれていません。底面の半径が図のどの部分に該当するかが分からないという人はほぼいないと思いますが、『母線ってどこ?』となる人はそれなりにいるのではないでしょうか?
底面の半径と母線の長さを図に書き込むと下図のようになります。
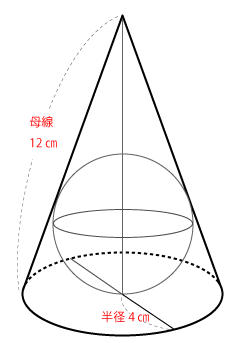
そして、この円すいを真横から見ると下図のようになります。
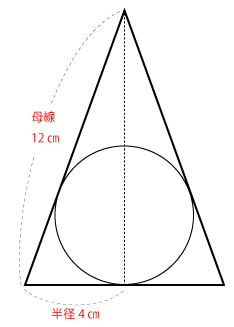
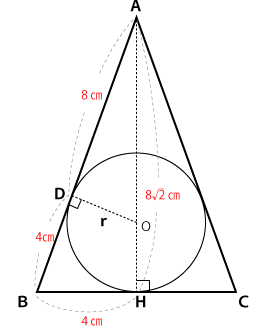
この図の三角形の各頂点をABCとし、円の中心から辺AB、BCに垂線を下ろして交わる点をD、Hとします。そうすると、ODは求めたい円(球)の半径となります。

三平方の定理より、以下の式が成り立ちます。
AB²=AH²+BH²
12²=AH²+4²
AH²=144-16
=128
AH=√128
=8√2
また、円の外のある1点から円に対して2つの接線を引いた場合、点から円の接点までの距離は等しくなるためBD=BHとなります。よって、BD=4cmとなり、AD=8cmだとわかります。
さらに△AODと△ABHは、内角が等しい相似な三角形で、その比は次の通り。
AH:AD=8√2:8
=√2:1
よって、BHとODの長さの比も√2:1となります。
BH:OD=√2:1
BH=√2OD
4=√2OD
OD=4/√2
=4√2/2
=2√2
よって、求めたい球体の半径は、2√2cm
※記載している解説の内容に誤りや不明な点があれば遠慮なくコメントください。

