この問題は平成30年4月入校の東京都立職業能力開発センター入校選考試験問題の問2の(1)と(2)の解答と解説です。
問1および、問2の(3)~(5)に関しては以下のページに解説をまとめているので参考にして下さい。
実際の試験の問題用紙は以下のページで確認することができます。
■目次
試験問題 問2(1)
図で、A、B、Cは直角三角形の各辺を1辺とする正方形です。Aの面積は324㎝²で、Bの面積は144㎝²です。このとき、直角三角形の面積は、何㎝²ですか。
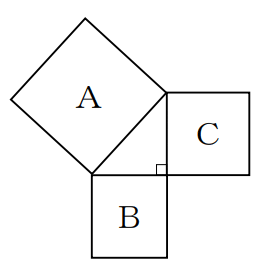
解答と解説
問2(1)の解答:36√5㎝²
この問題を解くには、三平方の定理を知っている必要があります。
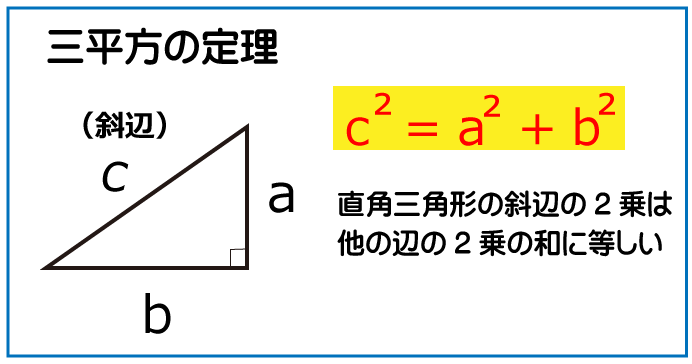
正方形Aの一辺の長さをa、Bの一辺の長さをbとした場合、それぞれの面積が324㎝²と144㎝²なので次の式が成り立ちます。
正方形Aの面積=a×a
324=a²
a=18
正方形Bの面積=b×b
144=b²
b=12
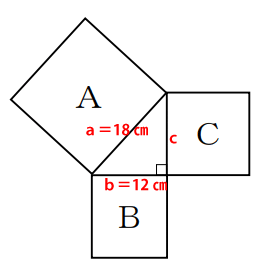
よって、三角形の高さにあたるCは三平方の定理より、下記の通りになります。
a²=b²+c²
18²=12²+c²
c²=324-144
c²=324-144
=180
c=6√5
よって、正方形ABCに囲まれた直角三角形の面積は次の通り。
三角形の面積=底辺×高さ÷2
=12×6√5÷2
=36√5㎝²
試験問題 問2(2)
縦の長さが横の長さより7㎝ 短い長方形があります。この長方形の面積が78㎝²であるとき、縦の長さは何㎝ですか。
解答と解説
問2(2)の解答:6㎝
求めたい長方形の縦の長さをNと仮定します。
縦の長さより横の長さが7㎝長いので、横の長さは次のようにあらわすことができます。
縦の長さ=N
横の長さ=N+7
長方形の面積が78㎝²なので、次の式が成り立ちます。
長方形の面積=横×高さ
78=(N+7)×N
N²+7N-78=0
上記の式を因数分解してNの値を求めます。足して7、掛けて-78になる値を探します。この場合、まずは掛けて「78」になる2つの数値を見つけることから始めると簡単に見つかる場合が多いです。掛けて78になる2つの数値は以下の4組があります。
1と78
2と39
3と26
6と13
この中で差が7になる組み合わせは6と13です。足して7にならないとダメなので6がマイナスになることがわかります。よって、因数分解すると次のようになります。
N²+7N-78=0
(N-6)(N+13)=0
よって、N=6、-13
辺の長さにマイナスはあり得ないので、求めたい長方形の縦の長さは6㎝となります。
※記載している解説の内容に誤りや不明な点があれば遠慮なくコメントください。

