次の各設問の解答を答えなさい。
[問題1]
2次関数y=3x²-6ax+12・・・①について、次の各設問に答えよ。
(1)2次関数①の頂点の座標が(3, -15)となるときのaの値を求めなさい。
①-3 ②-1 ③2 ④3
(2)a=2のとき、変域が0≦x≦3におけるyの最大値を求めなさい。
①12 ②6 ③3 ④9
(3)2次関数①がx軸と異なる2点で交わるときのaの値の範囲を求めなさい。
①-4<a<4 ②-2<a<2 ③a<-2, 2<a ④a<-4, 4<a
[問題2]
放物線y=x²と直線y=x+6との2つの交点をP、Qとする。原点をOとするとき、△OPQの面積を求めなさい。
①39 ②21 ③15 ④30
解答と解説
[問題1]の(1)解答:
2次関数y=3x²-6ax+12にX=3、y=-15を代入すればaの値は出てくる。
-15=27-18a+12
18a=54
a=3
解答:④
[問題1]の(2)解答:
a=2のとき、2次関数y=3x²-6ax+12は、y=3x²-12x+12 となる。よって、このグラフは下に凸のグラフで頂点が最小値になることがわかる。まずは、この頂点の座標を算出する。
y=3x²-12x+12
y=3(x²-4x)+12
y=3(x-2)²
よって、頂点の座標は、X=2、y=0だとわかる。この頂点(2, 0)より、X軸が遠くに離れた方がy軸の値は大きくなる。下のグラフを見て頂ければ分かると思う。
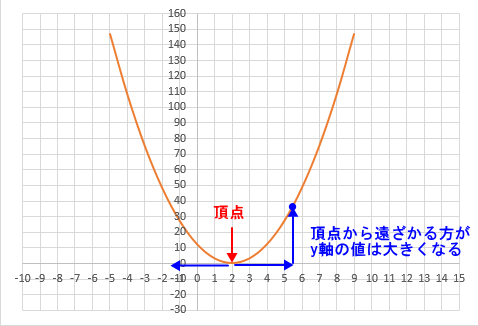
頂点(2, 0)から離れていくにつれy軸の値は大きくなる。よって、頂点のx座標が2なので、x軸が0≦x≦3の範囲であれば、x=3のときよりもx=0の方が頂点から離れている。このことより、x=0のとき、yが最大値となる。
y=3x²-12x+12
y=12
解答:①
[問題1]の(3)解答:
2次関数①がx軸と異なる2点で交わるということは、グラフの頂点のy座標が0未満でなければならない。[問題1]の(2)のときのように頂点の座標が(2, 0)であればx軸と1点しか交わらないことになる。
y=3x²-6ax+12
y=3(x²-2ax)+12
y=3(x-a)²-3a²+12
よって、y座標部分である「-3a²+12」が0よりも小さくなればいい。
-3a²+12<0
a²-4>0
(a+2)(a-2)>0
a<-2、a>2
解答:③
[問題2]の解答:
求めたいのは、下図の△OPQの面積。
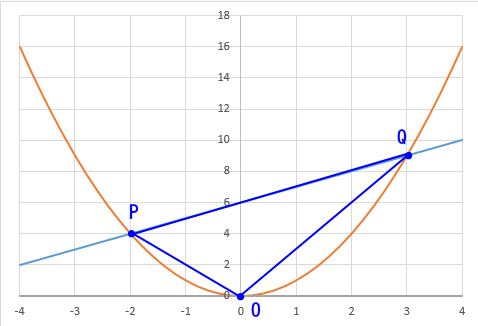
ここで、各線分の長さを求めて面積を求める方法もあるが、3つの点が(0,0)、(a,b)、(c,d)のとき、三角形の面積は次の公式で導くことができる。
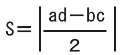
この公式を使用するためにOPQの3つの座標を求める。
まず、座標Oは、原点なので(0, 0)だとすぐに分かる。
次に、直線y=x+6を放物線y=x²に代入する。
x+6=x²
x²-x-6=0
(x-3)(x+2)=0
x=3、-2
よって、P点のX座標は-2、Q点のX座標は3だとわかる。そして、この2点のX座標を直線の式に代入すると、各々のy座標も求められる。
y=-2+6=4
P点の座標(-2, 4)
y=3+6=9
Q点の座標(3, 9)
これで3点OPQの座標がでた。これを面積を求める公式に代入すると
S=(12+18)/2=15
解答:③

