平成26年度に沖縄県で行われた職業訓練の選考試験で出題された試験問題と、その解答と解説です。 本ページでは数学問題の設問【2】のみ記載しています。数学問題の設問【1】、【3】~【5】に関しては、次のページを参照してください。
沖縄 職業訓練 平成26年度 試験問題と解答 問題【1】
沖縄 職業訓練 平成26年度 試験問題と解答 問題【3】
沖縄 職業訓練 平成26年度 試験問題と解答 問題【4】
沖縄 職業訓練 平成26年度 試験問題と解答 問題【5】
具志川職業能力開発校、浦添職業能力開発校 共通
【2】次の問に答えなさい。
[問題1] X²+4X-5 を因数分解せよ。
[問題2] a=4+√3、b=4-√3 のとき、ab-4bの値を求めよ。
[問題3] 4<√3a<4.5 を満たす自然数aの値を求めよ。
[問題4] 150n がある自然数の平方となるような、最小の自然数nを求めよ。
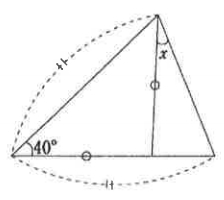
[問題5] 下図の∠Xの大きさを求めよ。
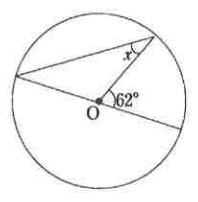
[問題6] 下図の∠Xの大きさを求めよ。
解答と解説
試験問題1の解答:(X-1)(X+5)
因数分解をする場合は、『たすき掛け』を利用します。たすき掛けの説明はここでは割愛しますが、『因数分解 たすき掛け』で検索すると詳細に解説してくれているサイトがたくさんあるのでそちらを参考にしてください。
この問題のように簡単な因数分解の場合は、たすき掛けを使用しない方が早い場合があります。
X²+aX+b
という二次方程式を因数分解する場合は、足してaになり、掛けてbとなるような2つの数値を探します。その2つの数値がcとdだったとすると、因数分解の結果は、次のようになります。
(X+c)(X+d)
よって、今回の問題であれば、足して4、掛けて-5となる2つの数値を考えます。私がよくやる方法は、まずは掛けて-5となる2つの数値を全て洗い出します。そうすると次の2つ組合せが出てきます。
1 -5
-1 5
更にこの2つの組み合わせの内、足して4となる2つの数値は、
-1 5
だと分かります。よって、因数分解の結果は、
(X-1)(X+5)
試験問題2の解答:-3+4√3
ab-4bにaとbの値を代入していきます。
ab-4b
=(4+√3)(4-√3)-4(4-√3)
=16-√3²-16+4√3
=16-3-16+4√3
=-3+4√3
試験問題3の解答:6
自然数とは、1,2,3,4・・・といった1から順に1ずつ足していった数値です。覚え方としては、自然界に存在する数値と覚えておけばいいでしょう。動物を数えるときに使う数値は、1,2,3,4・・・といった数値ですよね。1.5といった小数や、1/3といった分数は使いません。
解き方は色々ありますが、一番簡単と思われる解き方で記載します。aの範囲を求めたいので、問題の式を
xxx<a<○○○
という形に変形させることで、aの取り得る範囲が分かります。
4<√3a<4.5
上記の式を『xxx<a<○○○』の形に変形させるためには、まず全項に√3を掛けます。
4√3<√3√3a<4.5√3
4√3<√3²a<4.5√3
4√3<3√a<4.5√3
次に全項を3で割ります。
4√3/3<3√a/3<4.5√3/3
4√3/3<√a<1.5√3
次に全項を2乗します。
(4√3/3)²<(√a)²<(1.5√3)²
16√3²/9<a<2.25√3²
16×3/9<a<2.25×3
16/3<a<6.75
5.3333<a<6.75
これでaの取り得る範囲がわかりました。aは自然数なので、求めたいaの値は6だとわかります。
試験問題4の解答:6
『150n がある自然数の平方となる』という意味が分かり難いかもしれませんが、これはある自然数の2乗が150nになるということです。
ある自然数²=150n
または、
ある自然数=√150n
ということです。ここで1つこの問題を解くにあたり知っておきたい知識があります。
√144=√12²=12
√144=√3²×4²=12
上記の様に平方根内の数値(144)が自然数(12)になるためには、平方根内の数値が2乗の値に置き換えられる必要があります。これを知っていいればこの問題は簡単に解くことができます。
ある自然数=√150n
要は、150nが2乗の数値に置き換えることができればいいということです。まずは、nを無視し150に着目します。
150を分解していくと
150=2×75
=2×3×25
=2×3×5×5
=2×3×5²
上記の様に150という数値は『2×3×5²』になります。これが『2²×3²×5²』となって欲しいのです。よって、nが『2×3』であれば、『2²×3²×5²』という数値になってくれることが分かります。
n=2×3
よって、求めたい自然数nは6
補足
√150×6=√900=30
試験問題5の解答:X=30°
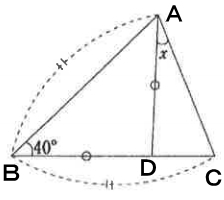
三角形ABDに着目
辺AD=辺BDなので、三角形ABDは2等辺三角形だとわかります。よって、次の角度が分かります。
∠DAB=40°
∠ADB=100°
∠ADC=80°
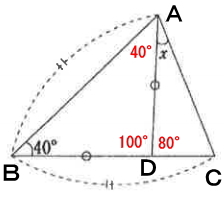
三角形ABCに着目
辺AB=辺BCなので、三角形ABDは2等辺三角形だとわかります。よって、次の角度が分かります。
∠A=∠C
∠CをY°とした場合、次の式が成り立ちます。
∠A=∠C
∠A=40°+X
∠C=Y
よって、
40°+X=Y ・・・(1)
また、三角形の内角の和は180°なので次の式が成り立ちます。
∠A+∠B+∠C=180°
40°+X+40°+Y=180°
X+Y=100 ・・・(2)
式(1)(2)の連立方程式を解けば求めたいXの値が出てきます。
40°+X=Y ・・・(1)
X+Y=100 ・・・(2)
式(1)を変形させます。
X-Y=-40 ・・・(1)
X+Y=100 ・・・(2)
式(1)+(2)をすると
X-Y=-40 ・・・(1)
X+Y=100 ・・・(2)
————————–
2X=60
X=30
よって、X=30°
試験問題6の解答:X=31°
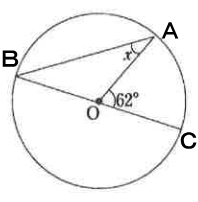
辺OBと辺OAは円の半径なので同じ長さになります。よって、三角形OABは二等辺三角形。このことより、次のことが分かります。
∠OAB=∠OBA
∠AOB=180-62=118
三角形の内角の和は180°なので、∠OAB+∠OBAは、180-118=62°だと分かります。よって、∠OABの角度は、
∠OAB=62÷2=31°
よって、X=31°
※解説の内容が不明、不十分というのがあればコメントをください。

