大阪 職業訓練 試験問題 数学-問3(平成27年2月20日実施) 普通課程

平成27年2月20日に大阪で実施された職業訓練の試験問題と解説です。大阪で行われる職業訓練の試験問題は、筆記試験ではなく毎回、選択方式ですが問題3は組合せやグラフと言った解くのに時間のかかる分野が出題されます。これらの過去問を繰り返し実施し、短時間かつ正確に解けるようにしておきましょう。

次の図で、直線ℓの式はＹ＝(－4/3)Ｘ＋8で、直線mと垂直に交わっています。点Aの座標を(－4,0)とするとき、次の各問の答えとして正しいものをア～オの中から1つ選び、記号で答えなさい。

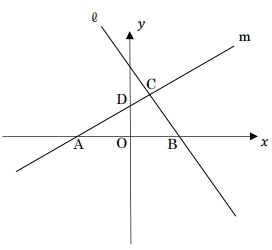
[問題１]直線mの式を求めなさい。

[問題２]三角形ABCの面積を求めなさい。

解答と解説

問題１の解説：

求めたい直線ｍの式を

　Ｙ＝ａＸ＋ｂ

と仮定します。
直線ｍは、直線ｌに直角に交わるということなので次の式が成り立ちます。(『※知っておく必要がある知識』を参照)

　(－4/3)×ａ＝－1
　ａ＝3/4

よって、直線ｍの傾きａは3/4と分かったのでＹ＝ａＸ＋ｂの直線式は次のようになります。

　Ｙ＝(3/4)Ｘ＋ｂ ・・・(３)

この時点で解答エオは消えましたね。
直線ｍは点Ａ(－4、0)を通るということなので(３)にこの値を代入し、ｂの値を求めます。

　Ｙ＝(3/4)Ｘ＋ｂ
　0＝(3/4)×(－4)＋ｂ
　0＝－3＋ｂ　
　ｂ＝3

よって、直線ｍの式は

　Ｙ＝(3/4)Ｘ＋3

解答：イ

問題２の解説：
三角形ＡＢＣの面積を求めるには、三角形の底辺となるＡＢの長さ、点ＣからＸ軸に対して垂直に下ろしたＣＤの長さを求める必要があります。

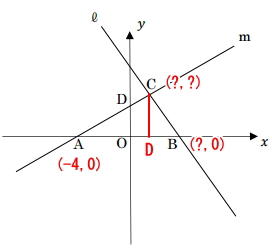
Ｂの座標を求める
Ｂの座標は、直線ｌがＸ軸と交わる点です。それは、直線ｌのＹ座標が0の点になります。よって、直線ｌの式のＹの値0を代入し、Ｘの値を求めます。

　Ｙ＝(－4/3)Ｘ＋8
　0＝(－4/3)Ｘ＋8
　(4/3)Ｘ＝8
　Ｘ＝8×(3/4)
　Ｘ＝6

Ｂ点のＸ座標が6、Ａ点のＸ座標が－4なので、ＡＢの長さは

　6＋4＝10

となります。Ａ点のＸ座標は－4ですが、ここでは距離を求めたいので－4ではなく4として計算しています。

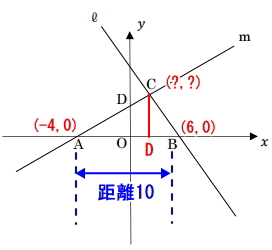
Ｃの座標を求める
ＣＤの長さは、点Ｃ点のＹ座標の長さになります。よって、点ＣのＹ座標を求めます。点Ｃは、直線ｌとｍの交点。

　直線ｌ　Ｙ＝(－4/3)Ｘ＋8
　直線ｍ　Ｙ＝(3/4)Ｘ＋3

上記2式からＹの値を求めるのですが、解き方は色々あるので自分のやりやすい方法で解いてください。下記は私が解く場合の方法です。

直線ｍの式を変形させます。左辺、右辺に4を掛け分数をなくし計算しやすくします。

　Ｙ × 4＝{(3/4)Ｘ＋3} × 4
　4Ｙ＝3Ｘ＋12
　3Ｘ＝4Ｙ－12
　Ｘ＝(4/3)Ｙ－4

このＸの値を直線ｌの式に代入しＹを求めます。

　Ｙ＝(－4/3)Ｘ＋8
　　＝(－4/3) × {(4/3)Ｙ－4} ＋ 8
　　＝(－16/9)Ｙ＋(16/3)＋24/3
　　＝(－16/9)Ｙ＋(40/3)
　Ｙ＋(16/9)Ｙ＝40/3
　(25/9)Ｙ＝40/3
　Ｙ＝(40/3)×(9/25)
　Ｙ＝(120/25)＝24/5

三角形ＡＢＣの面積を求める
三角形ＡＢＣの底辺ＡＢと、高さとなるＣ点のＹ座標がでてきました。

　ＡＢの長さ＝10
　ＣＤの高さ＝24/5

よって、三角形ＡＢＣの面積は

　三角形ＡＢＣの面積＝10×(24/5)÷2
　　　　　　　　　　＝24

解答：エ

※解説内容に不明な点があればコメント欄にコメントください。