下の図のように、同じ大きさの正三角形の白と黒のタイルを、同じ色のタイルがとなりあわないようにすき間なく並べ、1番目、2番目、3番目、・・・のように図形を作っていく。ただし、図形の外側には必ず白のタイルが並ぶこととする。
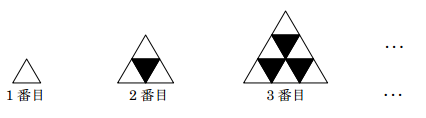
このとき、次の各問の答えとして正しいものをア~オの中から1つ選び、記号で答えなさい。
[問題1]5番目の図形に用いる白のタイルの枚数は何枚ですか。
ア 5枚
イ 8枚
ウ 10枚
エ 13枚
オ 15枚
[問題2]6 番目の図形に用いる白のタイルと黒のタイルの枚数の差は何枚ですか。
ア 4枚
イ 5枚
ウ 6枚
エ 7枚
オ 8枚
解答と解説
問題1の解説:
今回の問題は5番目の図形の白タイル数なので、図を実際に書いて力ずくで求めてもそんなに時間はかからない。ただ、10番目、20番目を求めよと言われた場合、図を各スペースも時間も無くなってしまうので、本来の解き方は知っておく方がよい。
まずは、問題の内容から現時点で分かっている内容を下記のように表にします。
n番目 1 2 3 4 5
白タイル数 1 3 6 ? ?
黒タイル数 0 1 3 ? ?
そして、これらの問題には必ず規則性が存在します。今回求める5番目の白タイル数の場合、白タイル数は、
1 ⇒ 3 ⇒ 6
と増えています。この規則性を考えると下記の様に1番目から2番目は2増え、2番目から3番目は3増えている。
1 ⇒ 3 ⇒ 6
+2 +3
この流れから3番目から4番目の増分は+4だと想定できる。本来であれば、このように2点の規則性から3点目を想定するのはよろしくない。できれば、4番目の図形を描いて3点以上の規則性を確認し、4点目、5点目を想定するようにしたい。心配な方は、4番目の図形を描いて増分が+4になることを確認した後、5番目を想定する様にしてください。
1 ⇒ 3 ⇒ 6 ⇒ 10 ⇒ 15
+2 +3 +4 +5
よって、求める解答は、15枚のオとなる。
解答:オ
問題2の解説:
問題1より、白タイルの5番目は15と分かっている。更に4番目と5番目の増分が+5だったので、次は+6だとすぐにわかる。
n番目 1 2 3 4 5 6
白タイル数 1 3 6 10 15 21
黒タイル数 0 1 3 ? ?
黒も同じように考えると、1番目と2番目の増分は+1、2番目と3番目の増分は+2。このことより、3番目以降も同様に+3、+4・・・と増えていくことが想定できます。よって、下表が完成する。
n番目 1 2 3 4 5 6
白タイル数 1 3 6 10 15 21
黒タイル数 0 1 3 6 10 15
問題は、6番目の図形に用いる白のタイルと黒のタイルの枚数の差なので、下記の枚数になる。
21-15=6枚
よって、求める解答は6枚のウ。
解答:ウ

