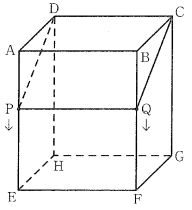
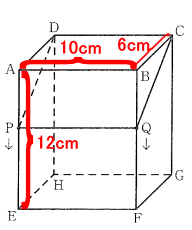
職業訓練試験問題右の図のABCD－EFGHは直方体で、AB＝10cm、BC＝6cm、AE＝12cm である。点Pは辺AE上を頂点Aから頂点Eまで、点Qは辺BF上を頂点Bから頂点Fまで動く点で、点P、Qはどちらも毎秒 2cm速さで動くものとし、2点P、Qはそれぞれ頂点 A、Bを同時に出発する。

このとき、次の各問の答えとして正しいものをア～オの中から１つ選び、記号で答えなさい。

[問題１]三角柱APD－BQCで2秒後の体積は何cm³ですか。

[解答群]
ア　12cm³
イ　20cm³
ウ　30cm³
エ　60cm³
オ　120cm³

[問題２]点P、Qがそれぞれ頂点 A、Bを出発してからx秒後の三角柱 APD－BQCの体積をy cm³とするとき、yをxを用いたできるだけ簡単な式で表したものはどれですか。ただし、0≦ x ≦6とします。

[解答群]
ア　y=12x
イ　y=20x
ウ　y=30x
エ　y=60x
オ　y=120x

[問題３]三角柱APD－BQCの体積と四角柱PEHD－QFGCの体積の差が三角柱APD－BQCの体積と等しくなるのは、点P、Qが出発してから何秒後ですか。

[解答群]
ア　4秒後
イ　5秒後
ウ　6秒後
エ　7秒後
オ　8秒後

解答と解説

問題１の解説：
職業訓練試験問題この問題を解くには三角柱の体積を求める公式を知っておかないと話にならない。

　三角柱の体積を求める公式 ＝ 底面積 ｘ 高さ・・・(１)

更に三角柱の底面は、三角形なので当然、底面積を求めるには三角形の面積を求める公式も知っておく必要がある。

　三角形の面積(底面積) ＝ 底辺 ｘ 高さ ÷ ２・・・(２)

まずは、三角柱の底面積を求めます。三角柱の底面を三角形APDとし、公式(２)を利用し、この三角形の面積を求めるのだが、その為には三角形の底辺と高さが必要になる。

　底辺をADとした場合、AD＝BC＝6cm

そうすると、高さは、APとなるのだが、Pは頂点Aから頂点Eに向かって秒速2cmで動く。問題は2秒後の体積を求めるので2秒間でPが動いた距離を求めればいい。よって、APの長さは次のようになる。

　高さAP＝2cmｘ2秒＝4cm

底辺と高さが分かったので、三角形APDの面積は次のようになる。

　三角形APDの面積＝底辺ｘ高さ÷2
　　　　　　　　 ＝6cmｘ4cm÷2
　　　　　　　　 ＝12cm² ・・・(３)

次に三角柱APD－BQCの体積を求めるのだが、公式(１)を利用します。底面積は、先ほど求めた(３)になる。更に三角柱APD－BQCの高さはABなので、10cmということがわかる。よって、三角柱の体積は次の式で求められる。

　三角柱の体積を求める公式＝底面積ｘ高さ
　　　　　　　　　　　　　＝12cm²ｘ10cm
　　　　　　　　　　　　　＝120cm³

よって、求める解答は120cm³のオ。

解答：オ

問題２の解説：
考え方は問題１と同じ。まずは、底面となる三角形APDの面積をもとめます。

　底辺をADとした場合、AD＝BC＝6cm
　高さAP＝2cm × Ｘ秒 ＝ 2Ｘ cm

よって、三角形の面積は、下記の通り。

　三角形APDの面積 ＝ 6cm × 2Ｘ ÷ 2 ＝ 6Ｘcm²

更に三角柱APD－BQCの高さはABなので、10cmと分かっている。よって、三角柱の体積ｙは次の通りになる。

　三角柱の体積ｙ＝底面積ｘ高さ
　　　　　　　　＝6Ｘcm² × 10cm
　　　　　　　　＝60Ｘcm³

よって、求める解答は、ｙ＝60ｘのエ。

解答：エ

問題３の解説：
問題より、下記の式が成り立つ。

　(四角柱PEHD－QFGCの体積)－(三角柱APD－BQCの体積)＝(三角柱APD－BQCの体積)・・(４)

Ｘ秒後の三角柱APD－BQCの体積は、問題２より、60Ｘと分かっているので、あとは、四角柱PEHD－QFGCの体積を求める必要がある。ここで必要になってくるのが四角柱の体積を求める公式。

　四角柱の体積を求める公式 ＝ 底面積 ｘ 高さ・・・(５)

更に四角柱の底面は、台形なので当然、底面積を求めるには台形の面積を求める公式も知っておく必要がある。

　台形の面積(底面積) ＝（上底＋下底）ｘ 高さ ÷ ２・・・(６)

まずは、この台形PEHDの面積(四角柱の底面積)を公式(６)を利用し求める。辺HDを台形の下底とした場合、辺HD＝AE＝12cmだと分かる。上底はPEになるのだが、Pは時間によって変わってくるので、Ｘ秒後の時間は次の様に表すことができます。

　AEの長さ＝12cm
　APの長さ＝2cm× Ｘ秒＝2Ｘcm

　よって、

　PEの長さ＝12cm － 2Ｘcm
　　　　　＝12-2X

これで、上底と下底の長さが分かりました。台形の高さは、EH＝BC＝6cmなので、次の様に台形PEHDの面積は求めることができます。

　台形PEHDの面積 ＝（上底＋下底）× 高さ ÷ ２
　　　　　　　　　＝（12-2X＋12）× 6 ÷ 2
　　　　　　　　　＝（24-2X）× 6 ÷ 2
　　　　　　　　　＝（144-12X）÷ 2
　　　　　　　　　＝ 72-6X

台形PEHDの面積が分かったので、四角柱PEHD－QFGCの体積も求めることができます。四角柱の体積は、公式（５）を利用します。四角柱PEHD－QFGCの高さはEF＝AB＝10cmと分かっているので、体積は次のようになる。

　四角柱PEHD－QFGCの体積 ＝ 底面積 ｘ 高さ
　　　　　　　　　　　　　＝（72-6X）ｘ 10
　　　　　　　　　　　　　＝ 720-60X

これで三角柱APD－BQCも四角柱PEHD－QFGCの体積も分かったので、式(４)を求めることができる。

　(四角柱PEHD－QFGCの体積)－(三角柱APD－BQCの体積)＝(三角柱APD－BQCの体積)
　(720－60X)－(60ｘ)＝(60ｘ)

この式を解くと求めたい秒数Xが出てくる。

　(720－60X)－(60ｘ)＝(60ｘ)
　720－60X－60ｘ＝60ｘ
　－60ｘ－60ｘ－60ｘ＝－720
　－180X＝－720
　X＝4

よって、求める解答は４秒後のアとなる。

解答：ア