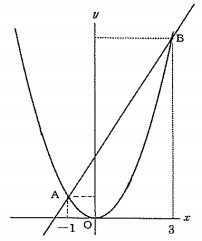
 放物線y=x²と関数y=ax+b(a、bは整数)が2点A、Bで交わっている。点Aのx座標は-1、点Bのx座標は3である。このとき、次の各問の答えとして正しいものをア~オの中から1つ選び、記号で答えなさい。
放物線y=x²と関数y=ax+b(a、bは整数)が2点A、Bで交わっている。点Aのx座標は-1、点Bのx座標は3である。このとき、次の各問の答えとして正しいものをア~オの中から1つ選び、記号で答えなさい。
[問題1]関数y=ax+bを求めなさい
ア y=2x+3
イ y=3x+5
ウ y=2-2
エ y=2x+5
オ y=-x+1
[問題2]原点Oを通り、△OABの面積を2等分する直線の式を求めなさい。
ア y=x
イ y=5x
ウ y=x/2
エ y=3x
オ y=2x
[問題3]座標1目盛りを1cmとしたとき、△OABの面積を求めなさい。
ア 12cm²
イ 18cm²
ウ 36cm²
エ 8cm²
オ 6cm²
解答と解説
問題1の解説:
点Aのx座標が-1と分かっているので、y=x²に代入すると、y座標がわかる。
y=x²
=(-1)²=1
よって、点A(-1, 1)となる。更に点BのX座標も3と分かっているので、同様にy=x²に代入すると、y座標がわかる。
y=x²
=(3)²=9
点B(3, 9)
点AとBの座標が分かったので、関数y=ax+bに代入すると求めたい式がわかる。
関数y=ax+bに点A(-1, 1)を代入
1=-1a+b ・・・(1)
関数y=ax+bに点B(3, 9)を代入
9=3a+b
b=-3a+9 ・・・(2)
式(2)を(1)に代入する。
1=-1a-3a+9
4a=8
a=2
a=2が分かったので、これを(1)もしくは(2)に代入しbの値も求めます。
b=-3a+9
b=-3×2+9
b=3
よって、関数y=ax+bは、y=2x+3となる。
解答:ア
問題2の解説:
この問題は絶対にまともに解こうとしてはいけない。まともにやると、10分程度かかってしまう。数学の勉強をするためであれば、もちろんまともに解くべきだが、職業訓練の選考試験でそれをやると時間はいくらあっても足りない。むしろ、この問題を作った人もそれを求めていない。もし、求めているのであれば△OABの面積を求める問題3が先に出題されるはずだ。それから2等分するというのが問題の流れになるべきです。
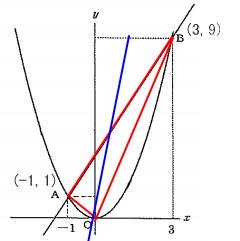 △OABを2等分するということは、だいたい右図の青線の様な直線になることが想像できる。
△OABを2等分するということは、だいたい右図の青線の様な直線になることが想像できる。
ということは、直線ABの式が問題1で求めたy=2x+3なので、直線の傾きは2xだとわかる。ここから言えることは、この直線と青色の直線が交わるためには、少なくとも傾きが2xよりも傾きが急でないといけない。
この時点で、解答群の選択肢、ア、ウ、オは消える。次にエのy=3xだが、傾きが2xより急なので直線ABと交わることは確実だが少し緩すぎる。仮にx=3を代入してみる。
y=3x=3×3=9
よって、y=3xの直線は、座標(3, 9)を通ることがわかる。この座標(3, 9)と言えば、点Bといっしょである。このことより、y=3xの直線は、直線OBのことなので、エも選択肢から外れる。よって、残りはイだけになるので、解答はイとなる。
解答:イ
問題3の解説:
3つの座標の内、1点が原点(0,0)を通り、残り2点を(a,b)、(c,d)とした場合、次の公式で面積が求められます。別の求め方として、2点間の距離と高さを求めて算出する方法もありますが、この公式を覚えておく方が圧倒的に簡単で早い。
この公式は3点の内、1点が原点を通らないと使えないと思われがちですが、3点とも原点を通らない場合はいずれか1点が原点を通るようにスライドさせればいいだけ。その方法は、下の補足事項の欄に記載しているので参考にして下さい。

よって、点A(-1, 1)、B(3, 9)なので、
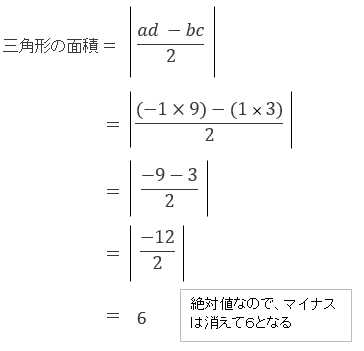
よって、求める解答は、6cm²のオ。
3つの座標の内、1点が原点(0,0)を通り、残り2点が(a,b)、(c,d)を通る場合の三角形の面積の求め方。
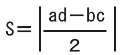
上記の公式を使用するには、下のグラフの様に三角形の3点の内いずれか1点が原点(0,0)になっている必要があります。
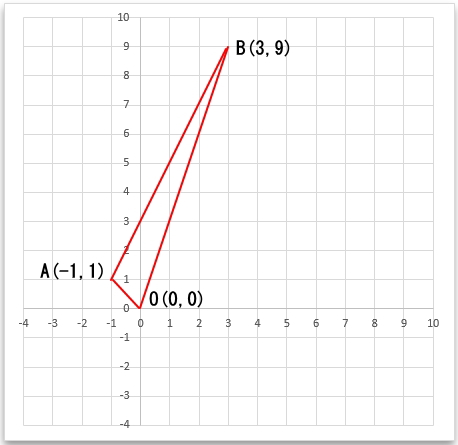
しかし、問題によっては、下のグラフの様に3点いずれも原点(0,0)を通っていない場合があります。
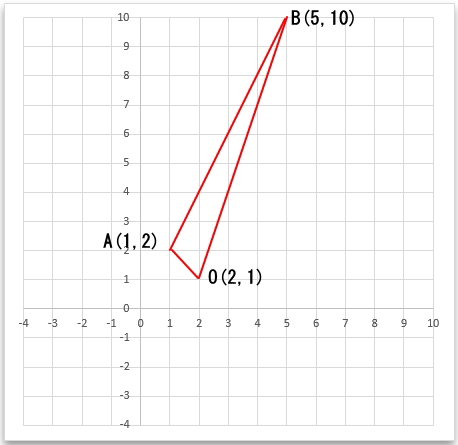
では、公式が使えないのか?
となりますが一手間加えることで公式が使用できるようになります。その方法とは、点A、B、Oのいずれかが原点にくるように3点をスライドさせればいいのです。
例えば、上のグラフであれば点OのX座標は2、Y座標は1となっています。これをX座標を-2、Y座標を-1方向にスライドさせると点Oが原点となります。この時、点Oだけをスライドさせるのではなく、点A、Bも同様にX座標を-2、Y座標を-1方向にスライドさせる必要があります。
スライドさせたのが下のグラフです。これで、公式が使用できるようになります。3点とも同じように移動させているので、三角形の面積が変わるようなことはありません。
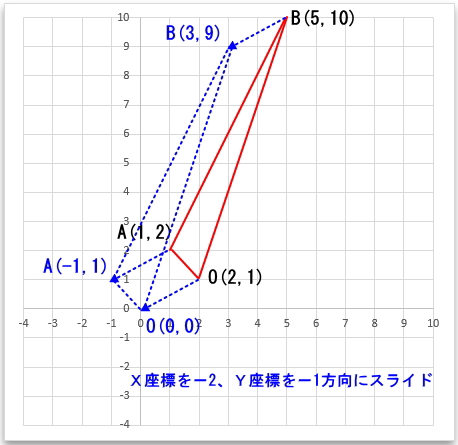
公式を忘れてしまった場合、次のような求め方もできます。下の三角形は、今回の設問を分かりやすくするために三角形部分のみを抜き出しました。
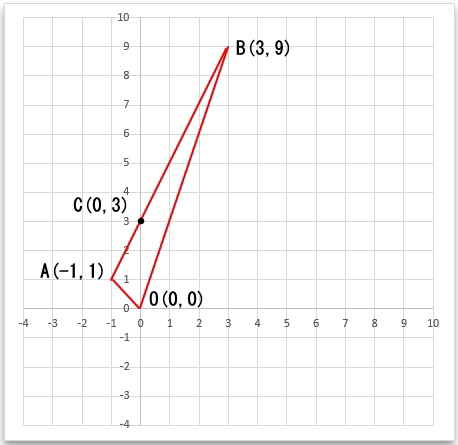
線分ABとY軸の交点をC点とします。線分ABは、設問1で求めたy=2x+3のグラフの一部で、このグラフとY軸との交点がC点なので、C点の座標は即座にC(0,3)と分かります。
何故なら、y=2x+3のグラフの切片3がY軸の交点だからです。切片って何?という人は、Y軸との交点なのでX=0を代入してY軸の値を出してもいいです。
y=2×0+3=3
さて、公式を使わずに解く方法ですが、三角形ACOと、三角形OCBの2つに分けて面積を求め、最後にこの2つを合計することで三角形AOBの面積を求めます。
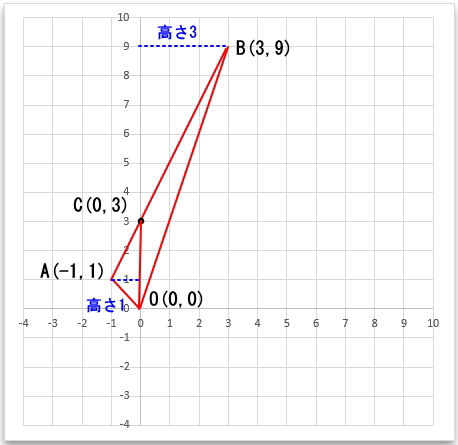
まずは、三角形ACOについて見ていきます。
三角形ACOの底辺は、線分OCでその長さは3。高さは、点AからY軸に垂直に下ろした線の長さになるので点AのX座標になります。X座標は、-1なのですがこれはあくまで座標位置であり、点AからY軸までの距離は1です。よって、三角形の面積の公式は『底辺×高さ÷2』なので、三角形ACOの面積は次のようになります。
三角形ACOの面積=3×1÷2=3/2
次に、三角形OCBについて見ていきます。
三角形OCBの底辺は、線分OCでその長さは3。高さは、点BからY軸に垂直に下ろした線の長さになるので点BのX座標になります。よって、点BからY軸までの距離は3です。よって、三角形の面積の公式は『底辺×高さ÷2』なので、三角形OCBの面積は次のようになります。
三角形OCBの面積=3×3÷2=9/2
よって、求めたい三角形OABの面積は、
三角形ACOの面積 + 三角形OCBの面積
=(3/2)+(9/2)
=12/2
=6
答え 6
解答:オ
※解説内容に不明な点があればコメント欄にコメントください。


はじめまして。
職業訓練校への試験を控え、こちらを参考に勉強している者です。解説が大変丁寧で、勉学から離れていた私にも理解しやすくとても感謝しております。
三角形の面積について、『いずれかの点を原点にスライドする方法』があるとの事で、ぜひご教授お願い致します。
シマさん
コメントありがとうございます。
『※補足』に記載したのでご確認下さい。
また、合わせて別の解き方も『※別解』に記載したので宜しければ参考にして下さい。
初めまして。
職業訓練の試験を控え、こちらの過去問をひたすら解いています。
問題2について、まともに解いてみました。
ーーーーーーーーーーーーーーーーーーーーーーーーーーー
三角形の頂点から対辺の中点にひいた線分は、
三角形の面積を二等分する。
これより、
△OABにおいて、頂点Oの対辺ABの中点を点Cとすると、
線分OCは、△OABの面積を二等分する直線となる。
点Cの座標を求める。
点Cのx座標は、点A(-1,1)、点B(3,9)の中間点であることから、
1 であることがわかる。
x=1のとき、y=2x+3 より、y=5
よって点C(1,5)
点O(0,0)と点C(1,5)をとおる直線は y=5x で表される。
ーーーーーーーーーーーーーーーーーーーーーーーーーーーーー
いかがでしょうか。
文字で表すと長いですが、
要するに、ABの中間点を求めるだけなので、
自分でグラフに書き込みながら考えると、すぐ解けます。
三十路様
コメントありがとうございます。
素晴らしいです。三十路様の考え方で全く問題ありません。
『三角形の頂点から対辺の中点にひいた線分は、三角形の面積を二等分する。』という点を知っているかどうかがポイントになりますね。皆さんにも参考の解き方になると思います。
ありがとうございます。