埼玉職業訓練試験問題[短期] 数学-問2(平成28年入校生)

平成28年度に埼玉県で実施された職業訓練(短期コース)の選考試験で出題された試験問題と、その解答と解説です。本ページでは数学問題の問題2(正式なテスト用紙上では設問6)のみ記載しています。その他の問題に関しては、以下のページを参照してください。

６. 次の問いに答えなさい。

[問題1]
１個７０円の消しゴムと 1 個１９０円のシャープペンシルを合わせて１５個買うと、代金が１，６５０円だった。このとき、消しゴムは何個買ったか。

[問題2]
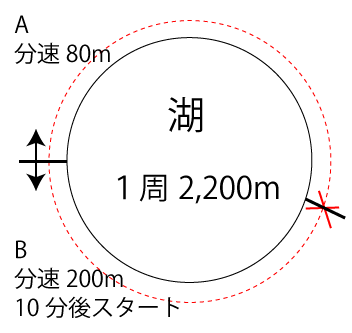
湖の周りに１周が２，２００ｍの道がある。この道をＡが分速８０ｍ、ＢはＡが出発してから１０分後にＡとは反対方向に分速２００ｍで走った。ＡとＢが出会うのはＡが出発してから何分後か。

試験問題１の解答：
求めたい消しゴムの個数をＹに置き換えて進めて行きます。

シャープペンシルと消しゴムを合わせて15個購入するということなので、シャープペンシルの数は次の様に表すことができます。

シャープペンシルの数＝15-Ｙ

消しゴム1個の値段が70円、シャープペンシル1本の値段が190円。総額1650円分購入したということなので、次の式が成り立ちます。

(70xＹ)+{190x(15-Ｙ)}＝1650

この式を解くと求めたい消しゴムの個数Ｘが求まります。

(70xＹ)+{190x(15-Ｙ)}＝1650
70Ｙ+(2850-190Ｙ)＝1650
70Ｙ-190Ｙ＝1650-2850
-120Ｙ＝-1200
Ｙ＝10

解答：10個

試験問題２の解答：
問題から分かっている点を図に落とし込むと下図のようになります。

この問題を解くにあたり、知っておかなければならない公式が以下の速度、距離、時間の関係です。

距離＝速度ｘ時間

この形が覚えにくいという人は、「速度＝距離/時間」だと覚えやすいのではないでしょうか？車やバイクのスピードメーターがまさにこの形(速度＝km/h)ですよね。

求めたい時間をｈとして計算を進めて行きます。

ＡがＢと出会うまでに走った距離
距離＝速度ｘ時間
　　＝80ｘｈ
　　＝80ｈ・・・(１)

ＢがＡと出会うまでに走った距離
ＢはＡが出発してから10分後に出発したので、Ｂが走った時間はＡが走った時間ｈより10分短いことになる。

Ｂが走った時間＝ｈ-10

よって、ＢがＡと出会うまでに走った距離は次の通り。

距離＝速度ｘ時間
　　＝200ｘ(ｈ-10)
　　＝200ｈ-2000 ・・・(２)

ＡとＢが出会うまでの時間
ＡとＢが走った距離の合計は、湖1周の2,200ｍになる。よって、次の式が成り立ちます。

2200＝80h+(200ｈ-2000)
2200＝80h+200ｈ-2000
80h+200ｈ＝2200+2000
280ｈ＝4200
ｈ＝15

よって、ＡとＢが出会うのはＡが出発してから15分後。

解答：15分後

関連記事