次の問に答えなさい。
[問題1] ある材料箱に、一つあたりの重さが均一のネジが複数本入っています。このネジ15本の重さを量ると33ｇでした。また、この材料箱から適当に取り出したネジの重さを量ると165ｇでした。このとき、ネジの本数は何本ですか。
[問題2] 50kmの道のりを毎時10kmの速さで往復するときにかかる時間は、何時間ですか。
[問題3] 2桁の自然数があります。この自然数は、一位の数の5倍より2大きく、十位の数字と一位の数字を入れかえてできる自然数は、もとの自然数より36大きくなります。このとき、もとの自然数を求めなさい。
[問題4] ある学校の今年度の生徒数は、昨年度に比べて、女子が7％減少し、男子が8％増加していますが、全体では昨年度より2人少なく、348人でした。このとき、今年度の男女別人数のうち、多い方の人数は何人ですか。
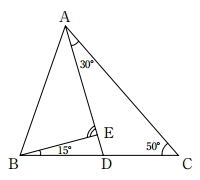
[問題5] 図のように、三角形ＡＢＣがあります。辺ＢＣ上に任意の点Ｄをとり、点Ａと結び、また、辺ＡＤ上に任意の点Ｅをとり、点Ｂと結びます。∠ＥＢＤ＝15°、∠ＣＡＤ＝30°、∠ＡＣＢ＝50°のとき、∠ＡＥＢは何度ですか。
解答と解説
試験問題１の解答：
ネジ15本の重さが33gなので、1本当たりの重さは次の通りです。
ネジ1本の重さ＝33÷15＝11/5
よって、ネジの総重量が165gの場合、そのネジの本数は次の通り。
165 ÷ (11/5)
＝165 × (5/11)
＝75
解答：75本
試験問題２の解答：
速度、距離、時間を求める問題は頻繁に出題されるので、下記の公式は必ず覚えておくようにしましょう。
速度 ＝ 距離 ÷ 時間
この問題はささいなひっかけがあります。設問には『50㎞の道のり』とありますが、そのまま公式の距離に50kmを入れてしまうと間違いになる。設問は往復となっているので、50㎞ではなく、100㎞になります。
片道にかかる時間を先に求めて最後に2倍しても問題ありませんが、ここでは、あらかじめ距離を100㎞として計算します。
速度 ＝ 距離 ÷ 時間
10 ＝ 100 ÷ 時間
時間 ＝ 100 ÷ 10＝10
解答：10時間
試験問題３の解答：
元の自然数の十の位の数字をＸ、一の位の数字をＹと仮定し計算します。
元の自然数の十の位の数字をＸ、一の位の数字をＹとした場合、元の自然数は、
(Ｘ × 10) ＋ Ｙ
となります。
例)
元の自然数が57の場合、十の位の数字が5、一の位の数字が7となります。これを元の数字に戻すには、下記の通り。
(5 × 10) ＋ 7 ＝ 57
元の自然数は、一位の数の5倍より2大きいということなので次の式が成り立ちます。
(Ｘ × 10) ＋ Ｙ ＝ (Ｙ × 5) ＋ 2
10Ｘ ＋ Ｙ ＝ 5Ｙ ＋ 2
10Ｘ － 4Ｙ ＝ 2
5Ｘ － 2Ｙ ＝ 1 ・・・(１)
次に、十位の数字と一位の数字を入れかえてできる自然数は、もとの自然数より36大きいということなので次の式が成り立ちます。
(Ｙ × 10) ＋ Ｘ ＝ (Ｘ × 10) ＋ Ｙ ＋ 36
10Ｙ ＋ Ｘ ＝ 10Ｘ ＋ Ｙ ＋ 36
9Ｙ － 9Ｘ ＝ 36
Ｙ － Ｘ ＝ 4 ・・・(２)
式(２)を式(１)へ代入すると、求めたいＸとＹの値が算出できます。計算の仕方は自分のやりやすいようにやって結構です。
式(２)を変形させる
Ｙ － Ｘ ＝ 4 ・・・(２)
Ｙ ＝ 4 ＋ Ｘ
これを式(１)へ代入する
5Ｘ － 2Ｙ ＝ 1 ・・・(１)
5Ｘ － 2(4 ＋ Ｘ) ＝ 1
5Ｘ － 8 －2Ｘ ＝ 1
3Ｘ ＝ 9
Ｘ ＝ 3
Ｘが出ました。このＸの値を式(２)へ代入し、Ｙの値も算出します。
Ｙ － Ｘ ＝ 4 ・・・(２)
Ｙ － 3 ＝ 4
Ｙ ＝ 7
よって、元の自然数は、37
解答：37
試験問題４の解答：
昨年の男子の人数をＸ人と仮定します。昨年の全校生徒数は今年よりも2人多かったので350人。よって、昨年の男子、女子の人数は次の通り。
昨年の男子の人数： Ｘ（人）
昨年の女子の人数： 350 － Ｘ（人）
今年の女子の人数は、昨年より7％減少しているということなので次の通り。
今年の女子の人数： 0.93(350 － Ｘ) ・・・(１)
更に今年の男子の人数は、昨年より8％増加しているといういことなので次の通り。
今年の男子の人数： 1.08Ｘ ・・・(２)
そして、今年の全校生徒数は348人。これは今年の男女の人数(１)(２)の合計に等しいはずなので次の式が成り立ちます。
348 ＝ 0.93(350 － Ｘ) ＋ 1.08Ｘ
この式を解くと昨年の男子人数Ｘが求まります。
348 ＝ 0.93(350 － Ｘ) ＋ 1.08Ｘ
348 ＝ 325.5 － 0.93Ｘ ＋ 1.08Ｘ
1.08Ｘ － 0.93Ｘ ＝ 348 － 325.5
0.15Ｘ ＝ 22.5
Ｘ ＝ 150
よって、昨年の男子と女子の人数は次の通り。
昨年の男子人数： 150人
昨年の女子人数： 200人(350－150)
しかし、知りたいのは今年の男女の人数。式(２)に昨年の男子人数Ｘ＝150 を代入して今年の男女人数を求めます。もちろん式(１)に代入してもかまわないが、式(２)の方がやや計算が楽。
今年の男子の人数： 1.08Ｘ ・・・(２)
＝1.08 × 150 ＝ 162人
全校生徒数が348人なので女子の人数は、
348 － 162 ＝ 186人
よって、求めたい今年の男女別人数の内、多い方の人数は、186人
解答：186人
試験問題５の解答：
分かっている角度をつぶしていくと簡単に求まります。
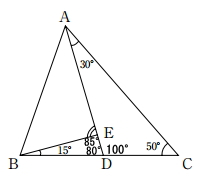∠ＣＡＤ＝30°、∠ＡＣＢ＝50°なので、∠ＡＤＣ＝100°となります。
また、∠ＡＤＣ＝100°なので、∠ＥＤＢ＝80°だとわかります。∠ＥＢＤ＝15°なので、∠ＢＥＤ＝85°とわかります。
よって、∠ＡＥＢ＝180－85＝95° となる。
解答：95°
