次の問に答えなさい。
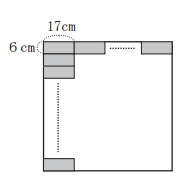
[問題1] 図のように、縦6cm、横17cmの長方形のカードを同じ向きに隙間なく並べて、できるだけ小さな正方形を作ります。このとき、必要なカードの枚数は全部で何枚ですか。
[問題2] YはXに反比例し、X=6のときY=-4となります。X=-3のときのYの値を求めなさい。
[問題3] 川の上流にA地点、下流にB地点があり、52㎞離れているAB間を船で往復します。A地点で出発してB地点へ向かう途中、エンジンを1時間停止して川の流れにまかせて移動したところ、B地点到着に4時間かかりました。次に、B地点からA地点へ向かう途中もエンジンを2時間停止して流され、A地点到着に9時間30分かかりました。この船の静水上の速さは毎時何kmですか。ただし、川の流れの速さは一定とします。
[問題4] 24で割ると商と余りが等しい数になる3桁の自然数は、全部でいくつありますか。。
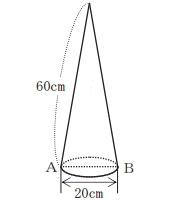
[問題5] 図のような、母線の長さ60cm、底面の直径AB=20cmの円錐において、点Aから円錐の側面を一回りして点Aに戻るように糸を巻きます。糸の長さが最も短くなるよに巻く時、糸の長さは何cmですか。
解答と解説
試験問題1の解答:
正方形を作るということは、縦と横の長さが等しくなるようにしなければならない。これを求めるには6と17の最小公倍数を求めればよい。
2つ以上の正の整数の共通な倍数(公倍数)のうち最小のものを最小公倍数という。
例) 3と4の最小公倍数
3の倍数 3 6 9 12 15 18 21 24 ・・・・
4の倍数 4 8 12 16 20 24 ・・・・
上記の通り、12と24は、3と4の共通の倍数になる。この共通の倍数の内、最小のものを最小公倍数といいます。よって、3と4の最小公倍数は、12。
それでは、6と17の最小公倍数をもとめます。最小公倍数の求め方はあるのですが、この程度の問題であれば書き出した方が早い。数学の好きなひとであれば、書き出さなくても即座に出てくる様な問題です。
1 )6 17
6 17
よって、最小公倍数は、1×6×17=102
計算の仕方が分からない人は、この程度であれば次のように力技で求めてもいい。
6の倍数 6 12 18 24 30 ~ 96 102
17の倍数 17 34 51 68 85 102
さて、6と17の最小公倍数は、102と分かりました。よって、1辺の長さが102cmとなる正方形が縦6cm、横17cmのカードで作れる最小の正方形になります。
カードの縦は6cmなので、102cmの正方形の縦には102÷6=17枚のカードが並ぶことになります。更にカードの横は17cmなので102cmの正方形の横には102÷17=6枚のカードが並ぶことになります。
よって、1辺が102cmの正方形内には、縦6cm、横17cmのカードが102枚(17×6)入る事になります。
解答:102枚
試験問題2の解答:
YはXに反比例するということなので、比例係数をaとした場合、次の式が成り立ちます。
Y=a/X ・・・(1)
X=6のときY=-4なので、上の式に代入すると比例係数(1/a)が分かります。
Y=a/X
-4=a/6
a=-24
よって、式(1)は次のようになります。
Y=(-24)/X
よって、X=-3を上の式に代入すれば求めたいYの値が出てきます。
Y=(-24)/X
Y=(-24)/(-3)
=8
解答:Y=8
試験問題3の解答:
速度=距離÷時間
この公式は必ず覚えておきましょう。公式を覚えられない人は、バイクや車のスピードメーターを思い出して下さい。スピードメータに速度の単位として『km/h』が表示されていると思います。これは、
速度=距離(km)/時間(h)
を表しています。公式そのままですよね。
求めたい、静水時の船の速度をVとします。
また、川の流れの速さをFとします。
◎下り(A地点⇒B点)について考える
かかった時間:4時間
距離:52㎞
4時間の内3時間は、船のエンジンをかけて移動
4時間の内1時間は、川の流れだけで移動
エンジンをかけて移動した距離
ここで注意が必要なのは、船のエンジンで移動しているとき。船の移動速度はVですが、実際の速度はこれに川の流れも加わるのでV+Fとなります。エンジンをかけて移動している場合を公式にあてはめると次のようになります。
V+F= 距離 ÷ 3
よって、エンジンをかけて移動した距離は、次の通り。
距離=(V+F)×3 …(1)
エンジンを停止中に移動した距離
次に、エンジンを止めている間ですが、船の移動速度は川の速度のみなのでFになります。これを公式にあてはめると次のようになります。
F= 距離 ÷ 1
よって、エンジンを停止している間に移動した距離は次の通り。
距離=F …(2)
そして、式(1)(2)の合計がAB間の距離になるので52㎞となります。
(V+F)×3 + F = 52
3V+4F=52 …(3)
◎上り(B地点⇒A点)について考える
かかった時間:9時間30分(9.5時間)
距離:52㎞
9.5時間の内7.5時間は、船のエンジンをかけて移動
9.5時間の内2時間は、川の流れだけで移動
エンジンをかけて移動した距離
船の進む方向にたいして、川は逆にながれているので船が進んでいる実際の速度はVではなくVから川の流れFを引いた速度になります。よって、これを公式にあてはめると次のようになります。
V-F= (距離) ÷ 7.5
よって、移動した距離は次の通り。
距離=(V-F) × 7.5 …(4)
エンジンを停止している間に進んだ距離
次にエンジンを停止した場合ですが、本来の船の進む方向に対して川の流れは逆。よって、船はB地点へ戻される方向に進むことになります。その際の速度はマイナスで表します。公式にあてはめると次の通り。
-F= (距離) ÷ 2
よって、移動した距離は次の通り。
距離=-2F …(5)
そして、式(4)(5)の合計がBA間の距離になるので52㎞となります。
(V-F) × 7.5 - 2F = 52
7.5V-9.5F=52 …(6)
次に式(3)と式(6)の連立方程式を解けば、求めたい静水時の船の速度Vを求めることができます。
3V+4F=52 …(3)
7.5V-9.5F=52 …(6)
この連立方程式の解き方は色々ありますが、自分が解きやすい解き方でとくとよい。
3V+4F=52 …(3)
75V-95F=520 …(6)
↓
285V+380F=4940 …(3)
300V-380F=2080 …(6)
↓
585V=7020
V=12
解答:12㎞/h
試験問題4の解答:
XをYで割ったときの商をM、余りをNとした場合、それぞれの関係は次の式で表すことができます。
X = Y × M + N
X=7
Y=2
M(商)=3
N(余り)=1
X = Y × M + N
7 = 2 × 3 + 1
設問は、Y=24、M=Nとなる数値です。
ただし、N(余り)は24より小さくなくてはなりません。24で割るのに余りが24以上あるのはおかしいですしね。
よって、式に当てはめると次のようになります。
X= Y × M + N
= 24 × M + N
= 24 × M + M = 25M (M < 24)
X=25M (M < 24)
次に、Xは3桁である必要があるので、条件として
100 ≦ X < 1000
これでXの条件が揃いました。
X=25M (M < 24)・・・(1)
100 ≦ X < 1000 ・・・(2)
この2つの条件を満たすXを求めればいいことになります。式(1)よりX=25Mなので、これを式(2)に代入すると次の条件になります。
100 ≦ 25M < 1000
これを2つに分けて考えます。まずは、左半分。
100 ≦ 25M < 1000
100 ≦ 25M
4 ≦ M
次に右半分。
100 ≦ 25M < 1000
M < 40
よって、Mの範囲は次の通りになります。
4 ≦ M < 40
しかし、ここで忘れてはだめなのが「M<24」の条件があったことです。よって、Mの範囲は次の通り。
4 ≦ M < 24
Mは、自然数なので、取り得る範囲は、
M=4、5、6 ~ 22、23
となり合計20個あることがわかります。
解答:20個
試験問題5の解答:
問題だけ読むと何のこっちゃ? となるような問題です。一度でも同様の問題を解いていれば分かる問題です。
要は、下図のように点Aを始点として円錐の側面に沿ってぐるっと糸を一周させ、再びAに戻ってきた場合の糸の長さですね。更に糸の長さが最も短くなるところをです。
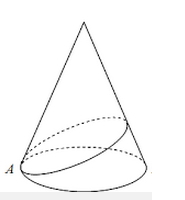
これは、円錐を展開するとすぐにわかります。円錐を展開すると下図の様に扇形になります。
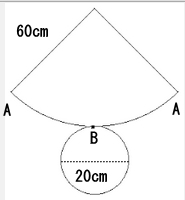
そして、Aから円錐の側面を回って再びAに戻ってくる最短距離は、下図のように点Aから点Aを直線で結んだ赤線だと分かります。よって、この赤線の長さを求めれば糸の長さも求まります。
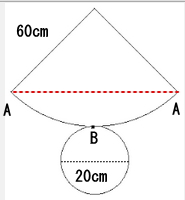
まず、この扇形の円弧(ABA)の長さを求めます。これは、円錐の底面の円の円周に等しいので次の円周を求める公式で求めることができます。
円の円周=直径 × Π
扇形の弧(ABA)の長さ=20×Π=20Π
次に、扇形の元の円の円周を求めます。半径が60cmなので円周は次の通り。
扇形の元の円の円周=60×2×Π=120Π
よって、円周120Πの内、20Π部分が扇形の弧の部分になるので、この扇形は、円周120Πの円を1/6(20Π/120Π)にしたものだとわかります。よって、扇形の中心角は下図のように60°(360/6)になります。
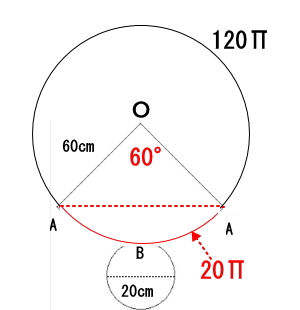
あとは、三角形OAAの辺AAの部分を求めれば赤点線の距離が求まるのですが、辺OAは円の半径なので等しい長さになります。よって、三角形OAAは、少なくてもニ等辺三角形か正三角形になる。ということは、二つの∠Aは同じ角度になるということです。
∠Oが60°なので、残り2角の合計は120°。よって、∠Aは60°だとわかり三角形OAAは正三角形となります。
このことより、辺AAの長さは半径と同じ60cmとなる。
解答:60cm

