平成27年2月20日に実施された大阪の職業訓練の選考試験問題と解説です。大阪で行われる職業訓練の試験問題は、筆記試験ではなく毎回、選択方式です。問題4は図形の問題が頻繁に出題されます。過去問を繰り返し実施し、短時間かつ正確に解けるようにしておきましょう。

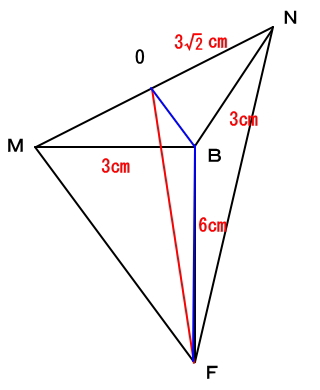
次の図で、1辺6cmの立方体ABCD-EFGH の辺ABとBCの中点をそれぞれ点M、点Nとして、この立方体を3点M、N、Fを通る平面で切り、2つの立体に分けることを考える。このとき、次の各問の答えとして正しいものをア～オの中から 1 つ選び、記号で答えなさい。

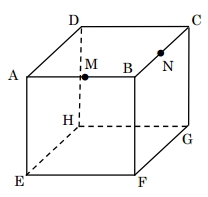
h27-2-20-f-q4-1

[問題１] 切り分けられた2つの立体のうち、小さい方の体積を求めよ。

[解答群]
ア　13cm³
イ　12cm³
ウ　11cm³
エ　10cm³
オ　9cm³

[問題２] 切断面FNMの面積を求めなさい。

[解答群]
ア　25/2 cm²
イ　25/3 cm²
ウ　25/4 cm²
エ　27/2 cm²
オ　25/4 cm²

[問題３] 切り分けられた2つの立体のうち、大きい方の立体について、さらに4点M、N、E、Gを通る平面で切り、2つの立体に分ける。このとき、小さい方の立体の体積を求めよ。

[解答群]
ア　50cm³
イ　51cm³
ウ　52cm³
エ　53cm³
オ　54cm³

解答と解説

問題１の解説：
小さい方の立体は、下図の赤線の三角すいになります。よって、三角すいの体積の求める公式を知っている必要があります。

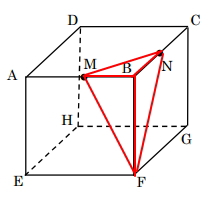
h27-2-20-f-q4-3

　三角すいの体積＝底面積×高さ×(1/3)

底面は三角形ＭＮＢです。点Ｍ、Ｎは辺ＡＢ、辺ＢＣの中点なので、ＭＢの長さ、ＮＢの長さは共に3cmだとわかります。よって、三角形ＭＮＢの面積は次の通り。

　三角形ＭＮＢの面積＝3×3÷2
　　　　　　　　　　＝4.5cm²

更に三角すいの高さは辺ＢＦなので6cmです。よって、三角すいの体積は公式より次の通り。

　三角すいの体積＝底面積×高さ×(1/3)
　　　　　　　　＝4.5×6×(1/3)
　　　　　　　　＝9cm³

解答：オ

問題２の解説：
切断面ＦＭＮは三角形です。よって、面積を求めるには底辺の長さと、高さを知る必要があります。

底辺をＭＮとした場合、高さは辺ＭＮの中点OからＦに引いた青線部分になります。

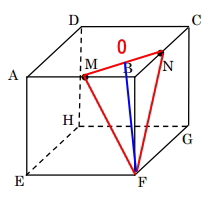
h27-2-20-f-q4-2

それでは、底辺の長さと高さを求めていきます。

底辺ＭＮの長さを求める
下図のように辺ＭＢ、ＢＮの長さは3cmと分かっています。また、∠ＮＢＭ＝90°なので、三角比が利用できます。

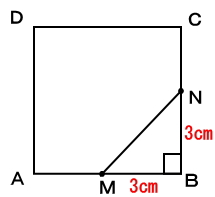
h27-2-20-f-q4-4

三角比
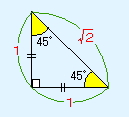
tokyo-sugaku-h25-01-q2-3

よって、三角比より、辺ＭＮ＝3√2

高さＯＦの長さを求める
三角形ＭＮＢの面積は、問題1で4.5cm²と分かっています。よって、次の式が成り立ちます。

　三角形ＭＮＢの面積＝底辺ＭＮ × 高さＯＢ ÷ 2
　4.5＝3√2 × ＯＢ ÷ 2
　9＝3√2 × ＯＢ
　ＯＢ＝3/√2

次に辺ＯＦの長さを求めるためにまずは、三角形ＯＢＦについて見ていきます。

h27-2-20-f-q4-5

∠ＯＢＦ＝90°なので、三平方の定理を使用することができます。

※三平方の定理
三平方の定理

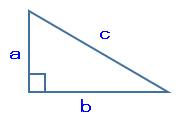
ｃ²＝ａ²＋ｂ²

が成り立つ。よって、これを三角形ＯＢＦにあてはめると

　ｃ²＝ａ²＋ｂ²
　ＯＦ²＝ＯＢ²＋ＢＦ²
　ＯＦ²＝(3/√2)²＋6²
　ＯＦ²＝9/2＋36
　ＯＦ²＝81/2
　ＯＦ＝9/√2

三角形ＦＭＮの面積を求める
三角形ＦＭＮの底辺ＭＮ＝3√2、高さＯＦ＝9/√2と分かったので、三角形ＦＭＮの面積は次の通り。

　三角形ＦＭＮの面積＝辺ＭＮ × 辺ＯＦ ÷ 2
　　　　　　　　　　＝(3√2) × (9/√2) ÷ 2
　　　　　　　　　　＝27/2

よって、三角形ＦＭＮの面積は、27/2 cm²

解答：エ

問題３の解説：
図のように図形ＭＢＮ－ＥＦＧ(赤線)について考えます。この図形ＭＢＮ－ＥＦＧは、最初の小さな図形三角すいＭＢＮ－Ｆも含まれるので、後程、図形ＭＢＮ－ＥＦＧから三角すいＭＢＮ－Ｆの体積（問題１）を引いて、今回求めたい図形の体積を求めます。

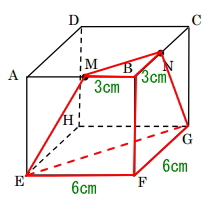
図形ＭＢＮ－ＥＦＧ(赤線)を延長させ、三角すいＥＦＧ－Ｐを作ります。

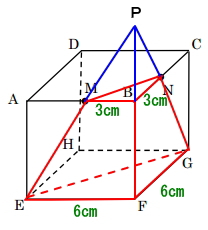
この三角すいＥＦＧ－Ｐと三角すいＭＢＮ－Ｐは相似な三角すいです。そして、その比は

　三角すいＥＦＧ－Ｐ：三角すいＭＢＮ－Ｐ＝6：3＝2：1

だと分かります。よって、

　辺ＰＦ：辺ＰＢ＝2：1

も成り立ちます。辺ＢＦの長さは6cmなので、辺ＰＢの長さをＸとした場合次の式が成り立ちます。

　辺ＰＦ：辺ＰＢ＝(Ｘ＋6)：Ｘ

この(Ｘ＋6)：Ｘが2：1となるはずなので

　(Ｘ＋6)：Ｘ＝2：1

これを解くと、

　(Ｘ＋6)：Ｘ＝2：1
　Ｘ＋6＝2Ｘ
　Ｘ＝6

辺ＰＢの長さが6cmと分かりました。よって、辺ＰＦの長さは12cmとなります。このことより、三角すいＥＦＧ－Ｐの体積は、

　三角すいＥＦＧ－Ｐの体積＝底面積 × 高さ ÷ 3
　　　　　　　　　　　　　＝三角形ＥＦＧの面積 × 辺ＰＦ ÷ 3
　　　　　　　　　　　　　＝(6×6÷2) × 12 ÷ 3
　　　　　　　　　　　　　＝72cm³ ・・・(１)

次に三角すいＭＢＮ－Ｐの体積を求めます。

　三角すいＭＢＮ－Ｐの体積＝底面積 × 高さ ÷ 3
　　　　　　　　　　　　　＝三角形ＭＢＮの面積 × 辺ＰＢ ÷ 3
　　　　　　　　　　　　　＝(3×3÷2) × 6 ÷ 3
　　　　　　　　　　　　　＝9cm³ ・・・(２)

よって、(１)－(２)をすれば、図形ＭＢＮ－ＥＦＧ(赤線)の体積が出てきます。

　(１)－(２)＝72－9＝63cm³ ・・・(３)

更にこの図形ＭＢＮ－ＥＦＧ(赤線)は、問題1で求めた最初の小さな図形の体積も含まれてしまっているので、問題1で求めた最初の小さな図形の体積を(３)から引くと、今回求めたい体積が出てきます。

　63cm³－9cm³＝54cm³

解答：オ

※解説の内容が分からない場合はコメント下さい。