問1~3に関しては以下のページに解説をまとめているので参考にして下さい。
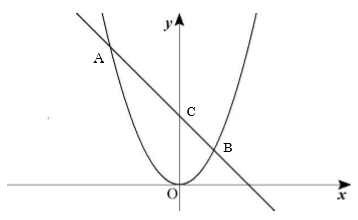
図のように、放物線y=x²/2上に、2点A、Bがあり、点Aのx座標は-4である。点Aと点Bのy座標の比は4:1 で、直線ABとy軸との交点をCとする。また、△OABの面積は12として以下の問いにア~オから選んで答えなさい。
[問題1] 点Bの座標を求めなさい。
[解答群]
ア (1,1) イ (2,1) ウ (1,2) エ (2,2) オ (2,3)
[問題2] △OBCの面積を求めなさい。
[解答群]
ア 10 イ 8 ウ 6 エ 5 オ 4
解答と解説
試験問題1の解答:エ
点Aの座標を求める
点Aのx座標は-4なので、y座標は次の通り。
y=x²/2
=(-4)²/2
=16/2
=8
点Aの座標(-4,8)
点Bの座標を求める
次に点Aと点Bのy座標の比が4:1ということは、点Bのy座標は点Aのy座標の1/4ということになります。よって、点Bのy座標は2となります。
よって、点Bのx座標は次の通り。
y=x²/2
2=x²/2
x²=4
x=±2
y=2のとき、x座標の取りうる値は2と-2の2通りあるが、点Bは直線と放物線がプラス側で交わる点なので、x=2となります。
点Bの座標(2,2)
試験問題2の解答:オ
辺OCを△OBCの底辺とすると、点Bからy軸に垂線を下した長さが△OBCの高さとなります。
点Cの座標を求める
直線ABの傾きをa、y軸との交点をbとした場合、直線の式は次のようになります。
y=ax+b
この直線は点Aと点Bを通ることから次のように傾きaと切片bが求まります。
y=ax+b
点Aの座標(-4,8)を通るので、
8=-4a+b ・・・(1)
更に点Bの座標(2,2)を通るので
2=2a+b ・・・(2)
式(1)(2)の連立方程式を解くとaとbの値が求まります。
8=-4a+b ・・・(1)
2=2a+b ・・・(2)
———————-
6=-6a
a=-1
「a=-1」を式(1)か(2)に代入します。
2=2a+b ・・・(2)
2=2x(-1)+b
b=4
よって、直線の式は次の通り。
y=-x+4
このことより、点Cの座標は次の通り。
点Cの座標(0,4)
△OBCの面積を求める。
点Cの座標が(0,4)なので、辺OCの長さは4と分かります。更に点Bからy軸に垂線を下した長さは点Bのx座標に相当するので、2だとわかります。
よって、△OBCの面積は次の通り。
△OBCの面積=4×2÷2=4
※解説を記載するまでもないと判断した問題に関しては、解説を記載せず解答のみを記載しています。もし、この問題の解説が欲しいというのがあれば、コメント欄に記載してください。また、記載している解説の内容も不明であれば遠慮なくコメントください。

