この問題は平成29年10月入校(試験実施日:平成29年8月25日)の大阪職業訓練短期過程の選考試験問題問4の解説です。特に難しい問題はありませんが、間違いやすい問題もあるのでこれらの過去問を繰り返し実施し、短時間かつ正確に解けるようにしておきましょう。
実際の試験の問題用紙は以下のページで確認することができます。
⇒平成29年10月入校 府立高等職業技術専門校 入校選考試験問題
問1、問3~問4に関しては以下のページに解説をまとめているので参考にして下さい。
この問題を解くのに必要な知識
- 因数分解(たすき掛け)の知識【必須】
- 円の面積を求める公式【必須】
- 円の円周を求める公式【必須】
- 四角形の面積を求める公式【必須】
- 円柱の表面積を求める公式【任意】
- 円柱の体積を求める公式【任意】
問4 試験問題
半径3㎝の円を底面とする高さ6㎝の直円柱Aがある。以下の問いにア~オの中から1つ選び、記号で答えなさい。ただし、円周率はπとする。
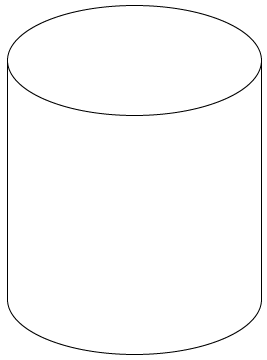
[問題1] 直円柱Aの半径と高さをそれぞれX㎝伸ばすと表面積がもとの直円柱の12倍の新しい直円柱Bができた。Xの値を求めなさい。
[解答群]
- √10
- 6
- 9
- 10
- 12
[問題2] 直円柱Bの体積は直円柱Aの体積の何倍になるか求めなさい
[解答群]
- 20倍
- 32倍
- 40倍
- 64倍
- 100倍
解答と解説
解答と解説を記載していきます。
解き方が分からないという人を少しでも減らすためにできる限り分かり易く必要以上に細かく順を追って解説している部分がありますが、実際の試験時は丁寧に計算し過ぎると時間のロスに繋がるため、自分の分かるところは効率よく解答していくようにしてください。
問題1の解答と解説
試験問題1の解答:ウ
まずは、問題文から分かっていることを図に書き込むと下図のようになります。
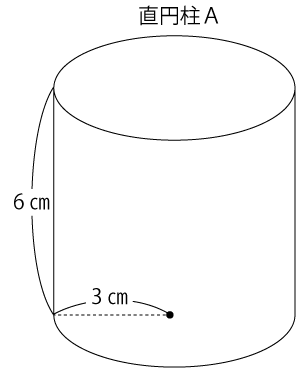
まずは、上図の現在の直円柱の表面積を求めていきます。
直円柱の表面積は円柱の上下にある底面積と側面の面積の合計になります。図を展開すると下図のようになります。
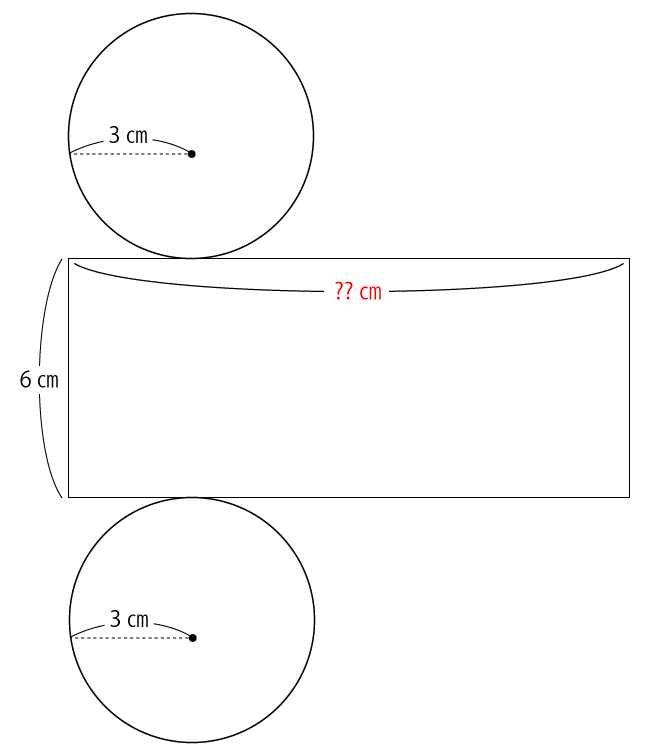
2つの円の面積は公式を知っていれば簡単に求まりますよね。
円の面積=半径×半径×π
円の面積=3×3×π=9π
これが2つあるので円の面積合計は18πとなります。
上下の円の面積合計=18π・・・①
次に円柱の側面にあたる四角形の部分ですが、横の長さが分かっていません。しかし、この横の長さは円の円周に等しいので、円周を計算することで求めることができます。
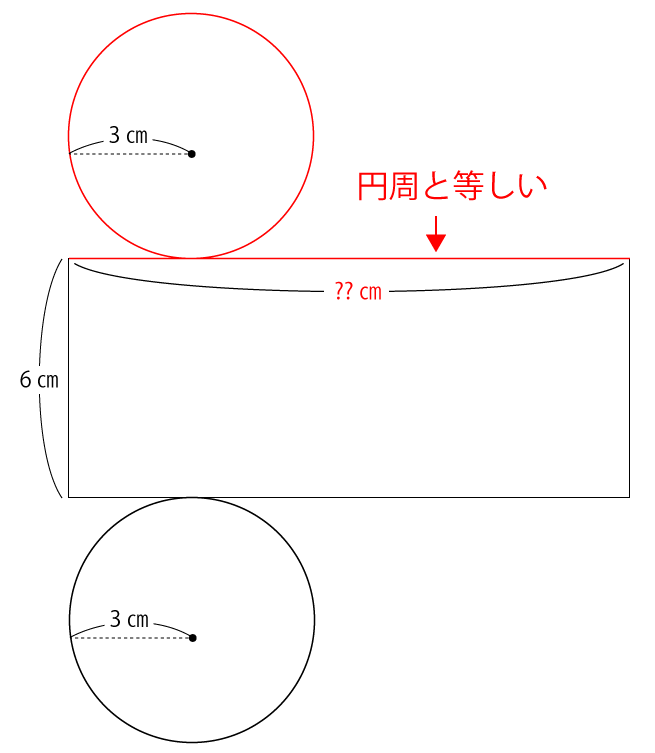
円の円周=直径×π
円の円周=(3+3)×π=6π
よって、直円柱の側面積は以下のようになります。
直円柱の側面積=6×6π=36π・・・②
直円柱の表面積は、①と②の合計なので次の通りになります。
直円柱Aの表面積=18π+36π=54π・・・③
問題は、直円柱Aの半径と高さをX㎝伸ばしたとき、表面積が元の直円柱の12倍になるとき、Xの値は何㎝かということでしたよね。半径と高さをX㎝伸ばしたときの直円柱Bの展開図は下図のようになります。
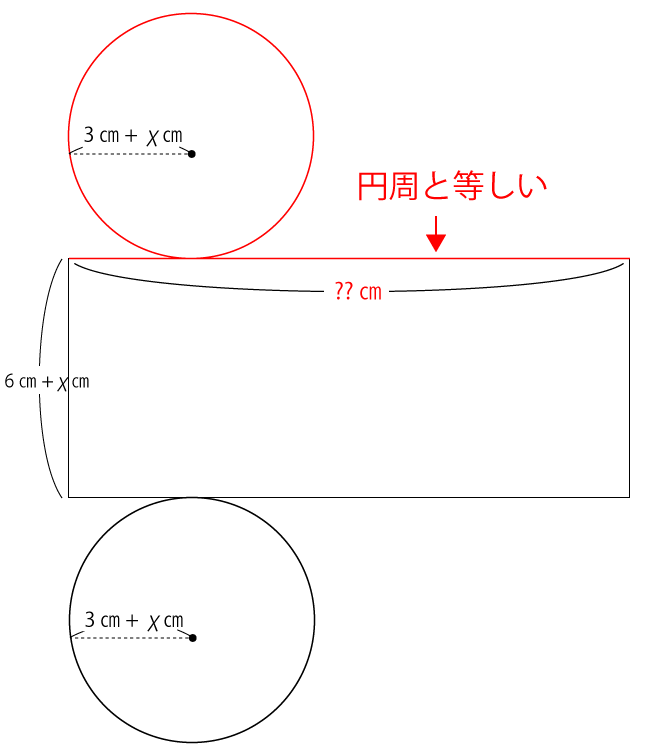
前回と同様に円の面積と側面の面積を求めます。
円の面積=(3+X)(3+X)π
これが上下に2つあるので合計は次の通り。
上下の円の面積合計=2(3+X)(3+X)π
=2(9+6X+X²)π
=(18+12X+2X²)π
側面の面積は次の通り。
円の円周={(3+X)+(3+X)}π=(6+2X)π
側面の面積=(6+X)(6+2X)π
=(36+18X+2X²)π
直円柱Bの表面積=(18+12X+2X²)π+(36+18X+2X²)π
=(54+30X+4X²)π・・・④
この④の値が③の12倍になるということなので以下の式が成り立ちます。
③×12=④
54π×12=(54+30X+4X²)π
648π=(54+30X+4X²)π
648=54+30X+4X²
4X²+30X-594=0
2X²+15X-297=0・・・⑤
この数式⑤を因数分解すると求めたい長さXがでてきます。ここで因数分解のやり方が忘れてしまったという人は、最悪、⑤の式に答えのア~オの数値を順に実際に当てはめて式が成り立つ数値を見つけ出しても構いません。
基本的にはたすき掛けを使用して解きます。
ここでは、たすき掛けの細かいやり方までは解説しませんが、やり方が分からない方はしっかりとできるようにしておいてください。
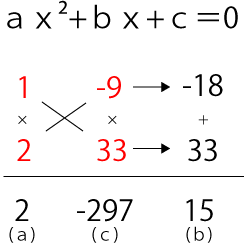
2X²+15X-297=0
(2X+33)(X-9)=0
よって、Xの値は-33/2と9の2つになります。しかし、長さにマイナスはあり得ないので、Xの長さは9となります。
問題2の解答と解説
試験問題2の解答:ウ
円柱の体積を求める公式は次の通りです。
円柱の体積=πr²h
上の公式を覚えていれば問題ありませんが、覚えていなくても『円柱の体積の求め方に関する補足』に記載している点を知っていれば体積を求めることができます。
問題1の解答より、直円柱Bの高さや円の半径は分かっており、直円柱ABは下図のようになります。
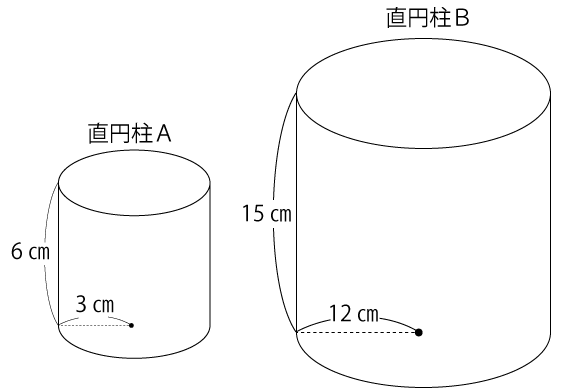
直円柱Aの体積=π×3²×6
=54π
直円柱Bの体積=π×12²×15
=2160π
2160π÷54π=40
よって、直円柱 B の体積は直円柱 A の体積の40倍となります。
円柱の体積の求め方に関する補足
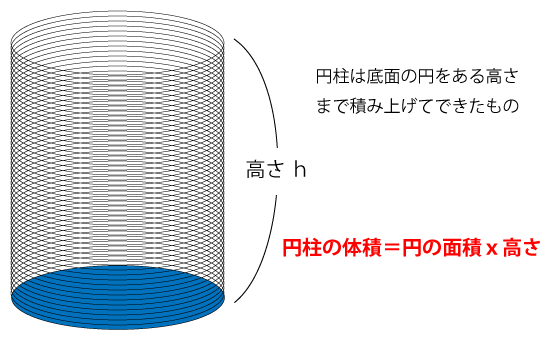
よって、円柱の体積は『円の面積×高さ』で求めることができます。
円の面積は半径をrとした場合、次のようになりますよね。
円の面積=半径×半径×π
=r×r×π
=πr²
そして円柱の高さをhとした場合、円柱の体積は次のようにあらわすことができます。
円柱の体積=円の面積×高さ
=πr²h
これが円柱の体積の公式と呼ばれるものです。これらのことを知っていれば公式を覚えていなくても自分自身で公式を導くことができます。
※解説を記載するまでもないと判断した問題に関しては、解説を記載せず解答のみを記載しています。もし、この問題の解説が欲しいというのがあれば、コメント欄に記載してください。また、記載している解説の内容に誤りや不明な点があれば遠慮なくコメントください。

