この問題は平成29年4月入校の東京都立職業能力開発センター入校選考試験問題の問2の(1)と(2)の解答と解説です。
問1および、問2の(3)~(5)に関しては以下のページに解説をまとめているので参考にして下さい。
実際の試験の問題用紙は以下のページで確認することができます。
■目次
試験問題 問2(1)
ある山道のA地点からB地点まで、毎時4kmの速さで登る時間と、毎時6kmの速さで下る時間とでは、かかる時間が80分違いました。A地点からB地点までの道のりは何kmですか。
解答と解説
問2(1)の解答:16km
この問題を解くには時間と速度と距離の公式を知っている必要があります。

登りにかかる時間をX、求めたいA地点からB地点までの距離をMと仮定し、問題文から分かっている点を図式化すると下図のようになります。注意点としては単位を時間に統一するために80分を時間に変換しています。(80分=80/60=4/3時間)
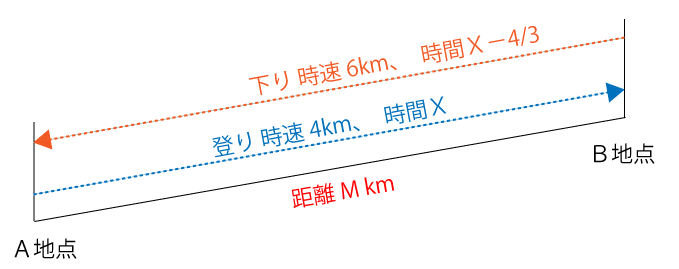
時間と速度と距離の公式より、登りと下りはそれぞれ以下の式であらわすことができます。
距離=速度×時間
M=4X・・・登り
M=6(X-4/3)
=6X-8・・・下り
登りの式より、X=M/4となり、これを下りの式に代入し距離Mを求めます。
M=6X-8
M=6×(M/4)-8
M=3M/2-8
3M/2-2M/2=8
M/2=8
M=16
よって、A地点からB地点までの距離は16km
試験問題 問2(2)
袋Aの中には白玉が2個と赤玉が3個、袋Bの中には白玉が3個と赤玉が3個入っています。袋Aから玉1個を取り出し、次に袋Bから玉を1個取り出します。このとき、取り出した玉が2個とも白玉となる確率はいくつですか。分数で求めなさい。
解答と解説
問2(2)の解答:1/5
この問題を解くには組み合わせ数を求める公式と確率の求め方を知っている必要があります。


以下の順で求めていきます。
解答までの流れ
- 袋Aと袋Bから玉1個ずつを取り出す組み合わせ数
- 取り出した玉が2個とも白玉である組み合わせ数
- 取り出した玉が2個とも白玉である確率
袋Aと袋Bから玉1個ずつを取り出す組み合わせ数
袋Aには白玉2個と赤玉3個の計5個の玉が入っています。その中から1個を取り出す組み合わせ数は5通り。あえて計算するまでもないと思いますが、計算式にすると次の通り。
₅C₁=(5×4×3×2×1)/{1×(4×3×2×1)}
=5通り
袋Bには白玉3個と赤玉3個の計6個の玉が入っています。その中から1個を取り出す組み合わせ数は6通り。あえて計算するまでもないと思いますが、計算式にすると次の通り。
₆C₁=(6×5×4×3×2×1)/{1×(5×4×3×2×1)}
=6通り
よって、袋Aから1個、袋Bから1個の玉を取り出した場合の総組み合わせ数は次の通り。
総組み合わせ数=5×6=30通り
取り出した玉が2個とも白玉である組み合わせ数
袋Aには白玉が2個入っています。よって、白玉が取り出される場合、このどちらかが取り出されることになるので2通りあることになります。
同様に袋Bには白玉が3個入っているので3通りあることになります。よって、白玉が取り出される組み合わせ数は次の通り。
白玉が取り出される組み合わせ数=2×3=6通り
実際に書きだすと以下の6通りになります。
1.袋A白1 袋B白1
2.袋A白1 袋B白2
3.袋A白1 袋B白3
4.袋A白2 袋B白1
5.袋A白2 袋B白2
6.袋A白2 袋B白3
取り出した玉が2個とも白玉である確率
袋Aから1個、袋Bから1個の玉を取り出す全事象の組み合わせ数が30通り、取り出した2個の玉が両方白玉である組み合わせ数は、6通りだと分かりました。よって、2個とも白玉が取り出される確率は次の通り。
2個とも白玉の確率=6/30
=1/5
※記載している解説の内容に誤りや不明な点があれば遠慮なくコメントください。

