この問題は平成29年4月入校の東京都立職業能力開発センター入校選考試験問題の問２の（５）の解答と解説です。

問１および、問２の（１）～（４）に関しては以下のページに解説をまとめているので参考にして下さい。

実際の試験の問題用紙は以下のページで確認することができます。

⇒都立職業能力開発センター入校選考試験問題(平成29年4月生)

試験問題 問２(５)

一辺が120mmの正方形ＡＢＣＤがあります。図のように、頂点Ｂが辺ＡＤの中点Ｅと重なるように折り曲げたとき、辺ＣＧの長さは何㎜ですか。

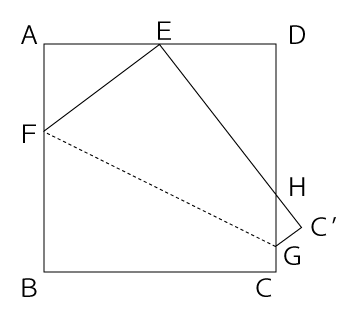
四角形を折り曲げた図

解答と解説

問２(５)の解答：15mm

まずは、問題文から分かっている点を図に書き込むと下図のようになります。

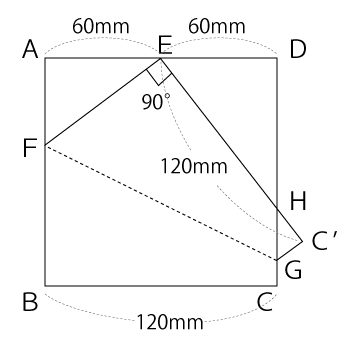
四角形を折り曲げた図

ここで気が付いて欲しいのが、△EAFと△HDEと△HC’Gの3つの三角形は相似な三角形だという点です。

この点に気が付けばこの問題は難しくありません。もし、なぜ、相似な三角形なのか分からない人は次章を参考にしてください。分かる方は読み飛ばして『辺CGの長さを求める』の章へいってください。

△EAFと△HDEと△HC’Gが相似三角形な理由

2つの三角形が相似な三角形になる条件は以下の3つの条件のいずれかに該当する場合です。

相似三角形の条件

  • ３組の辺の比がすべて等しい
  • ２組の辺の比とその間の角が等しい
  • ２組の角が等しい

そこで、まずは△EAFと△HDEに着目して見ていきます。

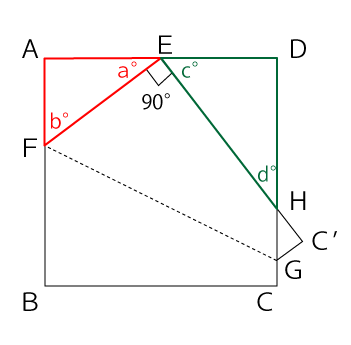
相似な三角形の証明

∠Aと∠D、∠FEHはすべて90°の直角です。よって、以下の3つの式が成り立ちます。

ａ＋ｃ＝90°・・・①
ａ＋ｂ＝90°・・・②
ｃ＋ｄ＝90°・・・③

ここで、①－②をします。

(ａ＋ｃ)－(ｃ＋ｄ)＝90°－90°
ａ－ｄ＝0
ａ＝ｄ

ａ＝ｄとなることが分かりました。よって、相似三角形の条件『２組の角が等しい』を満たすので△EAFと△HDEは相似な三角形と言えます。

次に△HDEと△HC’Gですが、∠DHEと∠C’HGは対角なので同じ角度になります。また、∠Dと∠C’は直角と分かっています。よって、相似三角形の条件『２組の角が等しい』を満たすので△HDEと△HC’Gも相似な三角形と言えます。

辺CGの長さを求める

AFの長さをａとした場合、FB＝FE＝120－ａとなります。

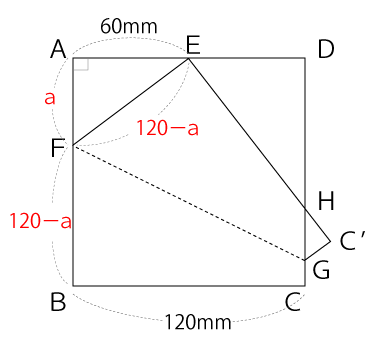
三平方の定理で辺の長さを求める

三平方の定理より、以下の式が成り立ちます。
FE²＝AF²＋AE²
(120－ａ)²＝ａ²＋60²
14400－240ａ＋ａ²＝ａ²＋3600
240ａ＝10800
ａ＝45

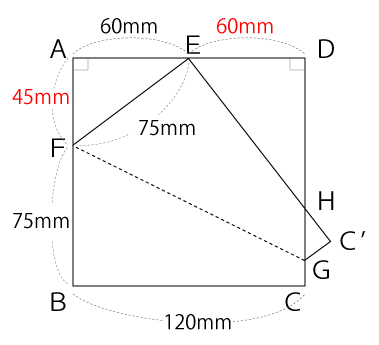
三平方の定理で辺の長さを求める

△EAFと△HDEは相似な三角形で、その比は次の通りです。

AF：DE＝45：60
　↓

AF：DE＝3：4

よって、EHの長さは次の通り。

EF：HE＝75：Ｘ
3：4＝75：Ｘ
3Ｘ＝300
Ｘ＝100

よって、EHの長さは100mm、HC’の長さは20mmだと分かります。

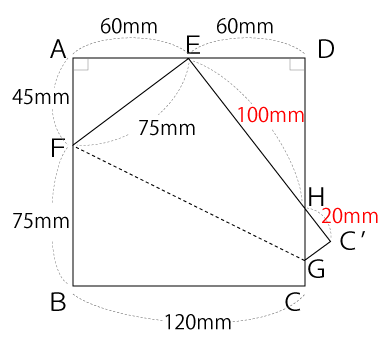
三平方の定理で辺の長さを求める

△EAFと△HC’Gは相似な三角形で、その比は次の通りです。

EA：HC’＝60：20
　↓

EA：HC’＝3：1

よって、C’Gの長さは次の通り。

AF：C’G＝45：Ｘ
3：1＝45：Ｘ
3Ｘ＝45
Ｘ＝15

よって、C’Gの長さは15ｍｍ。C’G＝CGなので求めたいCGの長さは15mm

※記載している解説の内容に誤りや不明な点があれば遠慮なくコメントください。