この問題は平成28年10月入校の東京都立職業能力開発センター入校選考試験問題の問2の(5)の解答と解説です。
問1および、問2の(1)~(4)に関しては以下のページに解説をまとめているので参考にして下さい。
実際の試験の問題用紙は以下のページで確認することができます。
試験問題 問2(5)
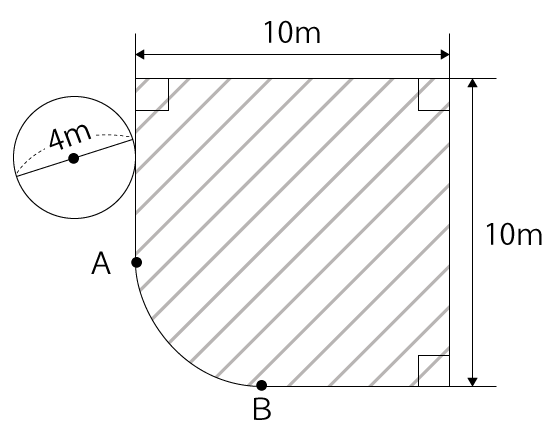
図のような図形があります。この図形の弧ABの長さは半径4mの円の円周の長さの4分の1です。このとき直径4mの円が斜線部分の図形の周りを転がりながら1周するとき、円が描く図形の面積は何m²ですか。
解答と解説
問2(5)の解答:128+24π m²
円が斜線部分の図形の周りを1周回った時に描く図形は下図の青色部分になります。
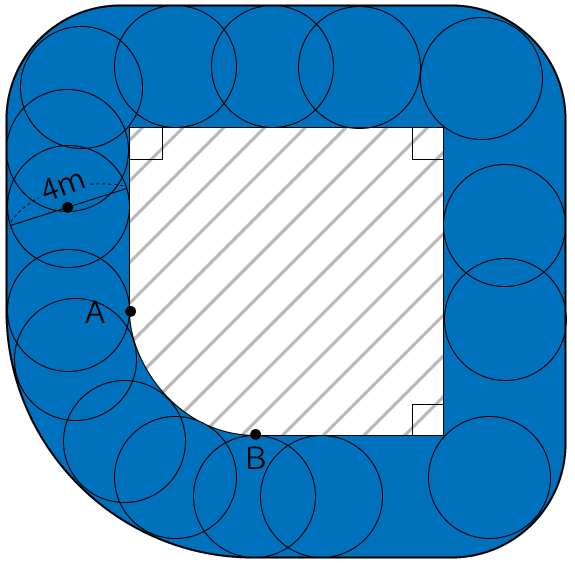
面積を求める場合は、下図ように赤色エリア、青色エリア、緑色エリアの3つに分けて考えていきます。
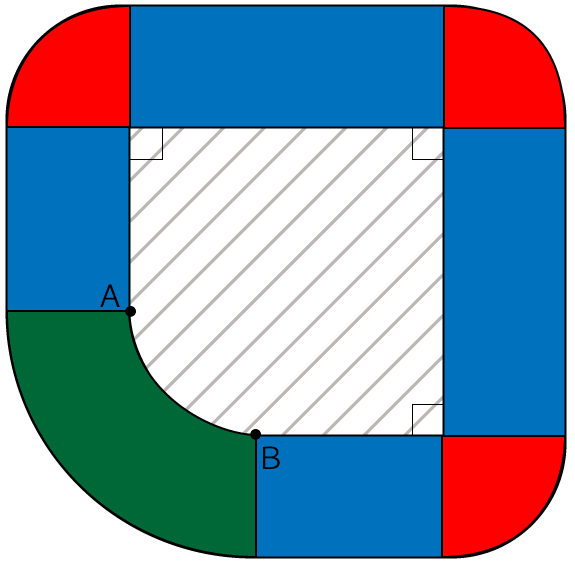
赤色エリアの面積
赤色エリアは半径4mの円の1/4の扇形が3つで構成されています。
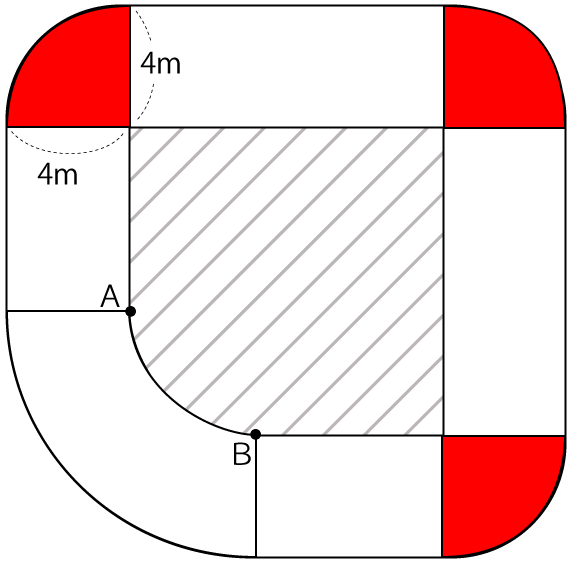
よって、赤色エリアの面積は次の通り。
赤色エリアの面積=(半径×半径×π×1/4)×3
=4×4×π×1/4×3
=12π m²・・・(1)
青色エリアの面積
下図の①~④の面積を順に求めていきます。
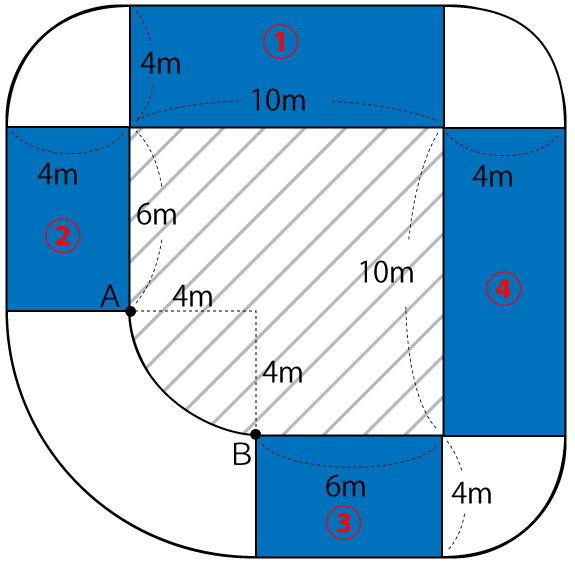
①の面積=4×10=40m²
②の面積=4×6=24m²
③の面積=6×4=24m²
④の面積=4×10=40m²
よって、青色エリアの面積は次の通り。
青色エリアの面積=40+24+24+40
=128 m²・・・(2)
緑色エリアの面積
緑色エリアの面積は、大きい方の扇形の面積から、小さい方の扇形の面積を引けば求まります。
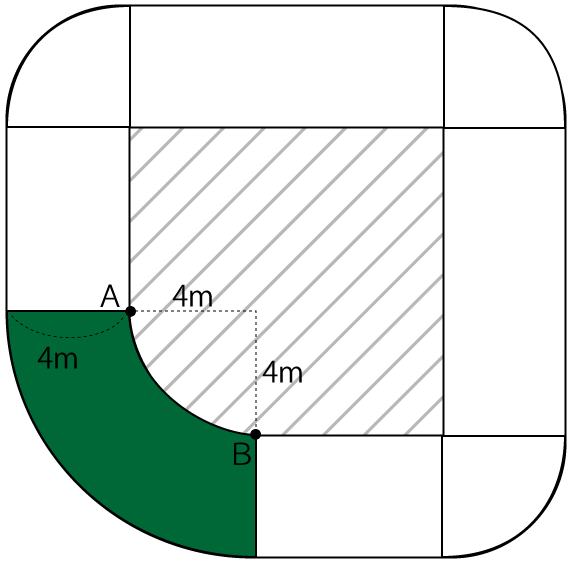
大きい方の扇形の面積=半径×半径×π×1/4
=8×8×π×1/4
=16π
小さい方の扇形の面積=半径×半径×π×1/4
=4×4×π×1/4
=4π
緑色エリアの面積=16π-4π
=12π・・・(3)
円が1周回ってできる図形の面積
円が1周回ってできる図形の面積は、『赤色エリアの面積(1)』と『青色エリアの面積(2)』と『緑色エリアの面積(3)』を合計すれば求まります。
円が1周回ってできる図形の面積=12π+128+12π
=128+24π m²
※記載している解説の内容に誤りや不明な点があれば遠慮なくコメントください。

