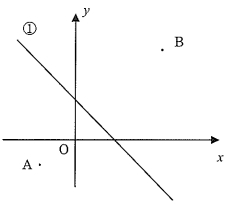
 右の図で、直線①は傾き-1、切片が2で、2点A、Bの座標はそれぞれ(-1、-1)、(3、3)である。このとき次の問に答えなさい。
右の図で、直線①は傾き-1、切片が2で、2点A、Bの座標はそれぞれ(-1、-1)、(3、3)である。このとき次の問に答えなさい。
[問題1]直線①についてyをxの式で表しなさい。
ア y=-x+2
イ y=-x-2
ウ y=x+2
エ y=x-2
オ y=-x
[問題2]2点A、Bを通る直線の式を求めなさい。
ア y=x+1
イ y=x
ウ y=x-1
エ y=-x+1
オ y=-x-1
[問題3]直線①とA、Bを通る直線の交点の座標を求めなさい。
ア (1/2、1)
イ (1/2、1/2)
ウ (1、1)
エ (1、3/2)
オ (3/2、3/2)
解答と解説
問題1の解説:
直線の式は、
y=(傾き)x+(切片)
で表されます。今回の設問では、傾きが-1、切片が2ということなので直線の式は次のようになります。
y=(傾き)x+(切片)
y=-x+2
よって、求める直線、y=-x+2のアとなります。
解答:ア
問題2の解説:
異なる2点(x1,y1),(x2,y2)を通る直線を求める公式は次の通り。
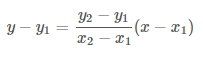
この式を覚えていれば単純に2点の値を代入するだけで、求めたい直線の式がでます。しかし、この公式を覚えていない場合は下記の直線の式に値を代入して求めていくしかありません。
y=(傾き)x+(切片)
計算する際は、傾きをa、切片をbに置き換えて計算します。
y=ax+b
今回の設問では、2点A(-1、-1)、B(3、3)を通るという事なので、これらの値を上記式に代入します。
A(-1、-1)
xに-1、yに-1を代入
-1=-a+b…(ア)
B(3、3)
xに3、yに3を代入
3=3a+b
b=3-3a…(イ)
式①に式②を代入します。
-1=-a+b
-1=-a+(3-3a)
-1=-a+3-3a
-4a=-4
a=1
aが求まったので、aの値を式(イ)に代入してbを求めます。もちろん式(ア)に代入してbを求めてもOK。
b=3-3a
b=3-3×1
b=0
これで、aとbが求まりました。この値を直線の式(y=ax+b)に代入すると、求めたい直線の式が出てきます。
y=ax+b
y=1x+0
y=x
よって、求めたい直線の式は、y=xのイ
解答:イ
問題3の解説:
問2で求めた直線y=xを直線②とした場合、直線①y=-x+2 との交点は、直線②の式を直線①に代入することで求められます。
直線① y=-x+2
直線② y=x
直線②式を直線①式に代入する
x=-x+2
2x=2
x=1
Xの値が求まったので、直線②の式にxの値を代入するとyの値も求まる。
y=x
y=1
よって、求めたい交点は、x=1、y=1の(1、1)になる。
解答:ウ
※解説の内容が分からない場合はコメント下さい。


[解答群]
ア y=x+2
イ y=-x-2
ウ y=x+2
エ y=x-2
オ y=-x
アとウ同じかと
あとう様
ご指摘ありがとうございます!
修正致しました。
誤) ア y=x+2
正) ア y=-x+2