平成30年 広島県高等技術専門校入校選考試験問題 問4、問5の解答と解説

試験問題 問４

次の数を小さい順に並べ替えなさい。

（１）－94　－1.5　0　－178　－2.3

（２）2√7　5　3√5　√53　√18

解答と解説

(１)の解答：－2.3　－94　－178　－1.5　0

分数があると、各数字を比較し難いので、分数でない形に変えます。

変え方は2つあり、1つは単純に分子÷分母をするだけです。割り切れなくても大小を比較できる桁数まで計算すれば構いません。今回のケースであればこの方法が妥当かもしれませんが、あえてもう一つの方法を紹介し、そちらで解説しておきたいと思います。理由としては同様の問題で汎用がきく場合が多いからです。

そのもう一つの方法は、全数字に同じ数を掛けて分数を無くす方法です。今回のケースであれば全数値に8を掛ければ分数は無くなります。また、全部の数値に同じ数を掛けるので大小は変わりません。

－94　－1.5　0　－178　－2.3

↓　8を掛ける

－18　－12　0　－17　－18.4

よって、小さい順に並べると次の通り。

－18.4　－18　－17　－12　0
↓　元の数値に変換
－2.3　－94　－178　－1.5　0

(２)の解答：√18　5　2√7　3√5　√53

平方根の大小を比較する場合は、ルート内に数値を戻してやると簡単に比較できます。

2√7＝√4√7＝√28

5＝√5²＝√25

3√5＝√9√5＝√45

√53

√18

あとは、ルートを無視して単純にルート内の数値だけで大小を比較すれば構いません。小さい順に並べると次の通りです。

√18　5　2√7　3√5　√53

試験問題 問５

次の各問いに答えなさい。

（１）現在、父親の年齢は43才、子どもの年齢は13才である。父親の年齢が子どもの6倍だったのは、何年前か。

（２）濃度12％の食塩水120ｇに水を加えたら、食塩水の濃度が7.2％になった。水を何ｇ加えたか。

（３）みかんを1人に3個ずつわけると28個あまり、1人に5個ずつ分けるとちょうど残りがなくなる。みかんは何個あるか。

（４）下のグラフは、200ｍ離れている2地点から、ＡさんとＢさんが向かい合って、同時に走り出すようすを表したものである。100ｍを、Ａさんは18秒、Ｂさんは12秒で走るとき、2人がすれ違うのは、走り出してから何秒後か。

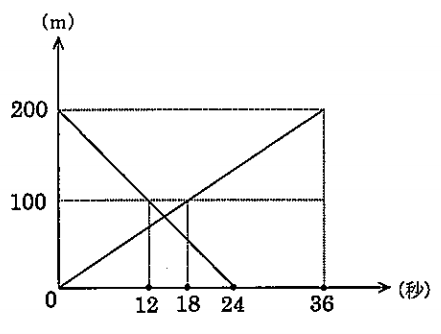
解答と解説

(１)の解答：7年前

求めたい何年前かの年数をＮ年と仮定した場合、以下の式が成り立ちます。

(43－Ｎ)＝(13－Ｎ)×6

この式を解けば求めたい年数Ｎが求まります。

(43－Ｎ)＝(13－Ｎ)×6
43－Ｎ＝78－6Ｎ
5Ｎ＝35
Ｎ＝7

よって、7年前

(２)の解答：80ｇ

この問題を解くには濃度を求める公式を知っている必要があります。

まずは、濃度12％の食塩水120ｇに含まれる食塩の量を求めます。

12＝Ｎ120×100
Ｎ＝(12×120)÷100＝14.4ｇ

ここに加える水の量をＭｇと仮定した場合、食塩の量は変わらないので公式より以下の式が成り立ちます。

7.2＝14.4(120＋Ｍ)

この式を解けば求めたい加えた水の量Ｍが求まります。

7.2＝14.4(120＋Ｍ)×100

7.2×(120＋Ｍ)＝14.4×100
7.2×(120＋Ｍ)＝1440
(120＋Ｍ)＝1440÷7.2
(120＋Ｍ)＝200
Ｍ＝80

よって、加えた水の量は80ｇ

(３)の解答：70個

求めたいみかんの個数をＮ個、分ける人数をＭ人と仮定します。

みかんを1人に3個ずつわけると28個あまるという点から以下の式が成り立ちます。

Ｎ＝Ｍ×3＋28
　＝3Ｍ＋28・・・①

さらに1人に5個ずつ分けるとちょうどになるということなので以下の式が成り立ちます。

Ｎ＝Ｍ×5
　＝5Ｍ・・・②

①＝②
3Ｍ＋28＝5Ｍ
2Ｍ＝28
Ｍ＝14

Ｍの値を式①もしくは式②に代入してＮの値を求めます。今回の場合であれば式②に代入した方が簡単ですよね。

Ｎ＝5Ｍ
　＝5×14
　＝70

よって、みかんの個数は70個

(４)の解答：14.4秒後

この問題は、2つのグラフの式を算出し交点座標から求める方法と、速度と距離と時間を求める公式を使って解く方法の2通りがあります。出題者側の意図としては前者を考えているようにも感じ取れますが、どちらで解いても構いません。

今回は、速度と距離と時間を求める公式を使って解く方法を最初に解説し、別解として後からグラフの交点から求める方法を解説していきます。

まずは、速度と距離と時間を求める公式を使って解く方法です。

Aさんの移動速度
速度＝100÷18＝50/9 ｍ/ｓ

Bさんの移動速度
速度＝100÷12＝25/3 ｍ/ｓ

AさんがBさんとすれ違うまでに進んだ距離をＮｍと仮定した場合、AさんとBさんの進んだ距離は以下で表すことができます。

Aさんが進んだ距離：Ｎ
Bさんが進んだ距離：200－Ｎ

よって、AさんがBさんとすれ違う時間は公式より次の通りとなります。

時間＝Ｎ÷50/9
　　＝9Ｎ/50・・・①

逆にBさんがAさんとすれ違う時間は次の通り。

時間＝(200－Ｎ)÷25/3
　　＝(200－Ｎ)×3/25
　　＝3(200－Ｎ)/25・・・②

走り出してからすれ違うまでの時間なので、AさんもBさんも時間は同じになります。よって①＝②となります。

9Ｎ/50＝3(200－Ｎ)/25
9Ｎ＝6(200－Ｎ)
9Ｎ＝1200－6Ｎ
15Ｎ＝1200
Ｎ＝80

Ｎの値を式①もしくは式②へ代入し、すれ違う時間を求めます。この場合であれば式①に代入した方が計算が簡単ですね。

時間＝9Ｎ/50
　　＝(9×80)/50
　　＝14.4

よって、二人がすれ違うのは走り出してから14.4秒後

(４)の別の解き方

ＡさんとＢさんの直線の式を求め、その交点が二人がすれ違う点になります。

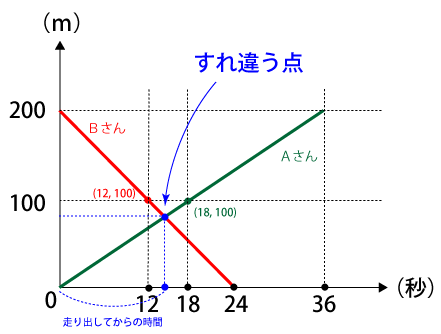
直線の式
ｙ＝ａＸ＋ｂ

Ａさんの直線の式

Ａさんの直線は原点を通るためｂ＝0となります。さらに傾きａが10018なので直線の式は次のようになります。

ｙ＝100Ｘ18
ｙ＝50Ｘ9・・・①

Ｂさんの直線の式

Ｂさんの直線はｙ軸との交点（切片）が200なのでｂ＝200となります。さらに傾きａが－10012なので直線の式は次のようになります。

ｙ＝－100Ｘ12＋200
ｙ＝－25Ｘ3＋200・・・②

直線の交点のＸ座標を求める

①式に②式を代入しＸの値を求めます。

50Ｘ9＝－25Ｘ3＋200

50Ｘ＝－75Ｘ＋1800
125Ｘ＝1800
Ｘ＝14.4

ＡさんとＢさんの直線の交点のＸ座標が求まりました。

よって、二人がすれ違うのは走り出してから14.4秒後

※記載している解説の内容に誤りや不明な点があれば遠慮なくコメントください。