平成30年 広島県高等技術専門校入校選考試験問題 問6、問7の解答と解説

試験問題 問６

次の各問いに答えなさい。

（１）Ｘ＝35、ｙ＝47のとき、2Ｘ－ｙ－(Ｘ－ｙ)の値を求めなさい。

（２）√2＝1.414として、√0.5の値を四捨五入して、小数第2位まで求めなさい。

（３）次の方程式を解きなさい。
Ｘ²＋12＝－8Ｘ

（４）次の連立方程式を解きなさい。
Ｘ＋2ｙ＝3
Ｘ＋4ｙ－7＝0

（５）次の式を因数分解しなさい。
p²－5pq－6q²

解答と解説

(１)の解答：35

2Ｘ－ｙ－(Ｘ－ｙ)
＝2×35－47－(35－47)
＝35

上記のように真面目に計算をしても構いませんが、計算時間を短縮するには以下のようにＸとｙに代入する前に計算してしまうことが大事。

2Ｘ－ｙ－(Ｘ－ｙ)
＝2Ｘ－ｙ－Ｘ＋ｙ
＝Ｘ
＝35

(２)の解答：0.71

√0.5
＝√1√2
＝1√2
＝11.414
＝0.707
＝0.71

(３)の解答：Ｘ＝－6、－2

Ｘ²＋12＝－8Ｘ
Ｘ²＋8Ｘ＋12＝0
(Ｘ+6)(Ｘ+2)＝0
Ｘ＝－6、－2

(４)の解答：Ｘ＝－1、ｙ＝2

Ｘ＋2ｙ＝3・・・①
Ｘ＋4ｙ－7＝0・・・②

式①－式②をします。

(Ｘ＋2ｙ)－(Ｘ＋4ｙ－7)＝3
－2ｙ＋7＝3
－2ｙ＝－4
ｙ＝2

ｙの値を式①に代入します。

Ｘ＋2ｙ＝3・・・①
Ｘ＋2×2＝3
Ｘ＋4＝3
Ｘ＝－1

よって、Ｘ＝－1、ｙ＝2

(５)の解答：(p－6q)(p＋q)

p²－5pq－6q²
(p－6q)(p＋q)

試験問題 問７

次の各問いに答えなさい。

（１）3点、Ａ(3,5)、Ｂ(－3,0)、Ｃ(1,－1)を頂点とする△ABCの面積を求めなさい。

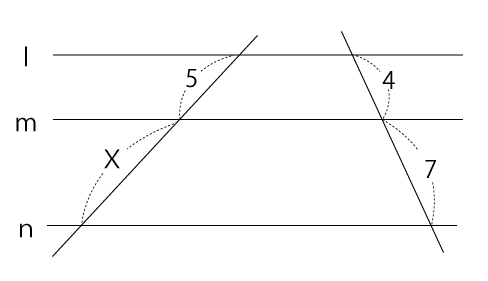
（２）下の図で、ｌとｍとｎが平行のとき、Ｘの長さを求めなさい。

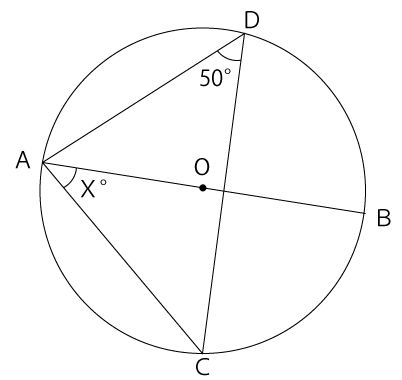
（３）下の図で、∠Ｘの大きさを求めなさい。

解答と解説

(１)の解答：13

点ＡＢＣを頂点とする△ＡＢＣをグラフ上に書き込むと下図のようになります。

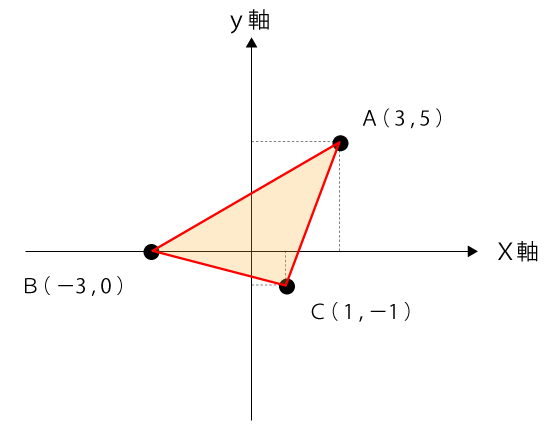
解き方はいくつかあり、最も短時間で解く方法は『平面上の三点を通る三角形の面積を求める公式』を使った解き方ですが、現役学生でない限り頭に入れている人は少ないと思うので、今回は一般的な解き方で解説します。

三角形の面積は、下図の2つの三角形に分けて考えていきます。

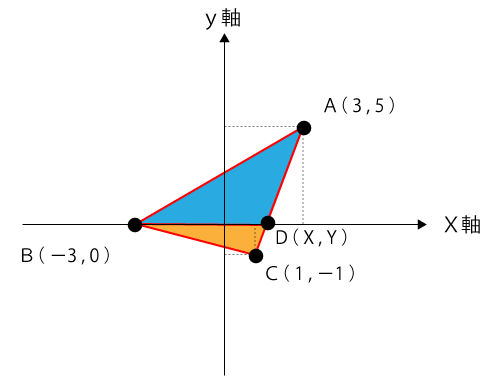
線分ACとＸ軸との交点Ｄの座標を求めます。

点ＡＣを通る直線の式
Y＝ａＸ＋ｂ

点Ａ(3,5)を通るのでＸ＝3、Ｙ＝5を代入する。
5＝3ａ＋ｂ・・・①

点Ｂ(－1,1)を通るのでＸ＝1、Ｙ＝－1を代入する。
－1＝ａ＋ｂ・・・②

式①－式②をして傾きａを求めます。
5－(－1)＝(3ａ＋ｂ)－(ａ＋ｂ)
6＝2ａ
ａ＝3

ａの値を式①へ代入し、切片ｂの値を求めます。
5＝3ａ＋ｂ
5＝3×3＋ｂ
ｂ＝－4

よって、点ＡＣを通る直線の式は次の通り。
Ｙ＝3Ｘ－4

この式にＹ＝0を代入しＸ軸との交点座標を求めます。
Ｙ＝3Ｘ－4
0＝3Ｘ－4
Ｘ＝43

よって、点Ｂと点Ｄの距離は次の通り。
点ＢＤ間の距離＝3＋43
　　　　　　　＝133

線分ＢＤは△ＡＢＤと△ＢＣＤの底辺となります。また、△ＡＢＤの高さは点ＡのＹ座標にあたるので5、△ＢＣＤの高さは点ＣのＹ座標の絶対値にあたるので1となります。よって、△ＡＢＤと△ＢＣＤの面積は次の通り。

△ＡＢＤの面積＝133×5÷2
　　　　　　　＝656

△ＡＢＤの面積＝133×1÷2
　　　　　　　＝136

△ＡＢＣの面積＝△ＡＢＤの面積＋△ＡＢＤの面積
　　　　　　　＝656＋136
　　　　　　　＝786
　　　　　　　＝13

(２)の解答：354

平行線ｌとｍに囲まれた台形と、平行線ｍとｎに囲まれた台形は4つの内角がすべて等しいので相似な台形図です。よって、以下の相似比が成り立ちます。

5：Ｘ＝4：7

これを解くとＸの長さが求まります。

5：Ｘ＝4：7
4Ｘ＝5×7
4Ｘ＝35
Ｘ＝354

(３)の解答：Ｘ＝40°

まずは、下図のようにＤＢ間に線を引き△ＡＢＤについ考えます。

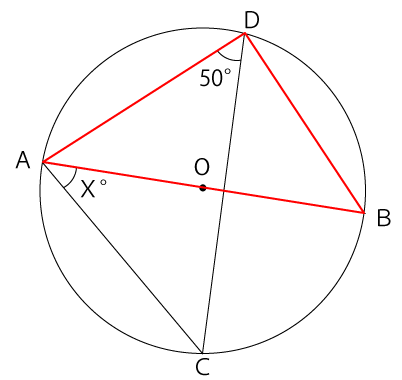
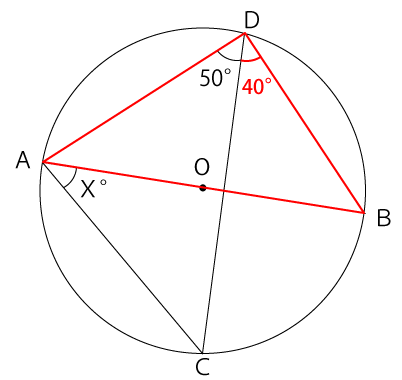
円の中心線を一辺とする三角形の円周角は必ず90°となります。よって、∠ＣＤＢ＝40°

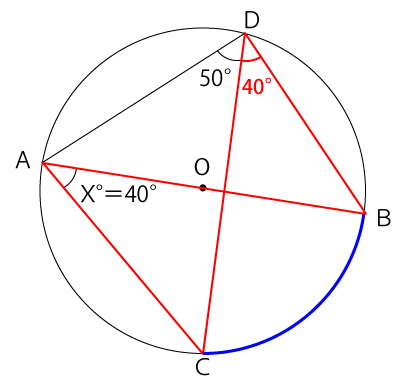
同じ弧をもつ円周角はすべて等しくなるので、同じ弧を持つＣＡＢとＣＤＢは、∠ＣＡＢ＝∠ＣＤＢとなりＸ＝40°だとわかります。

※記載している解説の内容に誤りや不明な点があれば遠慮なくコメントください。