次の各設問の解答を答えなさい。
[問題1]
![]()
①13 ②-7 ③7 ④-13
[問題2]
(3x²y)² × (-2xy³) を計算しなさい。
①-12x⁵y⁵ ②-18x⁵y⁵ ③18x⁵y⁵ ④-18x⁴y⁵
[問題3]
![]()
①15 ②14 ③18 ④30
[問題4]
x²-y²-4x+4を因数分解しなさい。
①(x+y+2)(x-y+2) ②(x-y+2)(x-y-2) ③(x+y-2)(x-y-2) ④(x+y-2)(x+y+2)
[問題5]
2次方程式x(x-9)=36を解きなさい。
①-4、9 ②-3、12 ③-12、3 ④-9、4
[問題6]
2つの不等式6x+1≧3x-5、x+4>3(x+1)を同時に満たすxの値の範囲を求めなさい。
![]()
[問題7]
-3<x<2、-4<y<3のとき、xy=kのとりうる値の範囲を求めなさい。
①-9<k<12 ②-12<k<6 ③-8<k<12 ④-9<k<6
解答と解説
試験問題1の解答:
{3×3-4x(-8)}/2 - {2×3-3x(-8)}/4
=(9+32)/2-(6+24)/4
=41/2 - 15/2
=26/2
=13
答え:①
試験問題2の解答:
(3x²y)² × (-2xy³)
=(9x⁴y²) × (-2xy³)
=-18x⁵y⁵
答え:②
試験問題3の解答:
![]()
一見計算が面倒なように見えるが下記のように並び順を変えて前2つ、後ろ2つの( )どうしを最初に計算すると簡単。
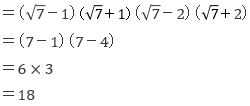
答え:③
試験問題4の解答:
これは、真面目に因数分解してもいいが、因数分解された解答の方を逆に展開して、設問と同じ式になるものを探した方が早い。
設問の式は、x²-y²-4x+4 である。ここで着目するのは、「-y²」の部分。「-y²」になるためには、( )内のyがどちらか一方はプラスで、他方がマイナスとならなければならない。
よって、この時点で②と④は選択肢から消える。残りは、①と③だけなのでどちらか一方だけ計算して展開をする。設問の式と一致すればそれが正解。一致しなければもう一方の方が正解となる。
では、実際に①(x+y+2)(x-y+2)を展開してみる。
x²-xy+2x+xy-y²+2y+2x-2y+4
=x²+4x+3xy-y²+4
設問の式と一致しない。よって、求める解答は③だと分かる。実際の試験のときはこれで解答すればよいが、念のため③(x+y-2)(x-y-2)も展開してみる。
(x+y-2)(x-y-2)
x²-xy-2x+xy-y²-2y-2x+2y+4
=x²-y²-4x+4
設問の式と一致する。よって、③が正解は正しい。
答え:③
試験問題5の解答:
x(x-9)=36
x²-9x-36=0
(x-12)(x+3)=0
よって、求める解答は12と-3となる。
因数分解に自信のない人は、解答群の値を実際に設問の式に代入して、式が成り立つものを見つける方法でも早い。
答え:②
試験問題6の解答:
6x+1≧3x-5 ・・・(1)
x+4>3(x+1) ・・・(2)
まずは、(1)を計算してみる。
6x+1≧3x-5
3x≧-6
x≧-2
次に、(2)を計算してみる。
x+4>3(x+1)
x+4>3x+3
-2x>-1
x<1/2
よって、xは、-2以上かつ、1/2未満とわかる。これを不等式になおすと、
-2≦x<1/2
答え:④
試験問題7の解答:
それぞれの最大値、最小値を掛け合わせ、その結果から最小になるものと、最大になるものをピックアップすればいい。
(xの最小値)x(yの最小値) = (-3)x(-4) = 12
(xの最大値)x(yの最大値) = 2x3 = 6
(xの最小値)x(yの最大値) = (-3)x3 = -9
(xの最大値)x(yの最小値) = 2x(-4) = -8
よって、xyの掛けあわせた結果が最大となるのは12、最小になるのは-9
-9<k<12
答え:①

