長崎 職業訓練 選考試験問題 数学-問2(平成30年度入校)

試験問題 問２

次の各設問の回答として正しいものをア～エの中から選びなさい。

2次関数 Ｙ＝Ｘ²－2ａＸ＋8ａ－12・・・(イ)がある。次の各設問に答えなさい。

（１）２次関数(イ)の頂点の座標を求めなさい。

（２）ａ＝1としたときの、２次関数(イ)の 0≦Ｘ≦4 の最大値をＭ、最小値をｍとする。Ｍ－ｍ の値を求めなさい。

（３）2次関数(イ)がＸ軸と異なる2点で交わるとき、定数ａの値の範囲を求めなさい。

（４）2次関数(イ)がＸ軸と異なる2点で交わるとき、その交点をＡ，Ｂとする。線分ＡＢの長さが4√3となる定数ａの値を求めなさい。

解答と解説

(１)の解答：エ

この問題を解くには平方完成の知識が必要です。二次関数の頂点座標を求める公式を知っていればさらに早く解くことができます。

二次関数Ｙ＝(Ｘ＋ａ)²＋ｂ という式があった場合、その二次関数の頂点座標は(－ａ,ｂ)となります。よって、平方完成を利用してこの形式に変形させます。

Ｙ＝Ｘ²－2ａＸ＋8ａ－12
　＝(Ｘ－ａ)²－ａ²＋8ａ－12・・・①

よって、二次関数の頂点座標は（ａ,－ａ²＋8ａ－12）となります。

(２)の解答：イ

(１)の解答より、頂点座標にａ＝１を代入すると、頂点座標は次のようになります。

頂点(1,－5)

そして、二次関数の式は次の通り。

Ｙ＝(Ｘ－1)²－5

二次関数の式はＸ²の係数がプラスなので二次関数は上開きのグラフとなります。

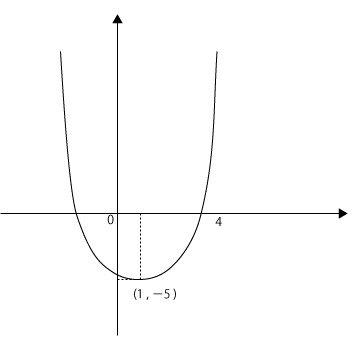
よって、Ｙが最小値となるのは頂点となります。よって、最小値ｍは－5となります。

最小値ｍ＝－5

次に最大値Ｍですが、2次関数の上開きのグラフの場合、最小値である頂点のＸ座標から遠い位置にあるＸ座標ほどＹの値は大きくなります。

よって、頂点のＸ座標は1なので、Ｘ＝0のときよりもＸ＝4のときの方が遠い位置にあり、Ｙの値も大きいと瞬時にわかります。よって、最大値Ｍは次の通り。

Ｙ＝(Ｘ－1)²－5
　＝(4－1)²－5
　＝9－5
　＝4

最大値Ｍ＝4

よって、Ｍ－ｍは次の通り。

Ｍ－ｍ＝4－(－5)＝9

(３)の解答：エ

『Ｘ軸と異なる2点で交わる』と言う表現が誤解を生みやすく、『Ｘ軸と異なる？Ｙ軸と交わるということ？』と思ってしまう人もいあるかもしれませんが、これは『Ｘ軸上の異なる2点で交わる』ということです。

Ｘ軸上の異なる2点で交わるには、二次関数の頂点がＸ軸よりも下にある必要があります。頂点がＸ軸上にある場合は、1点しか交わらず、Ｘ軸よりも上にある場合はＸ軸と1点も交わりません。

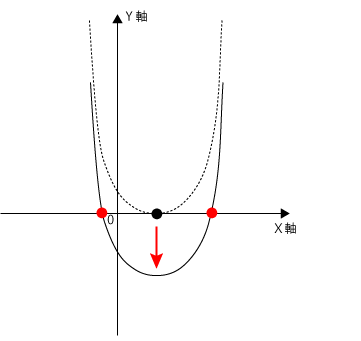
二次関数の頂点座標は（１）で求めており、頂点（ａ,－ａ²＋8ａ－12）だと分かっています。このＹ座標が0よりも小さくなる必要があるので、以下の式が成り立ちます。

－ａ²＋8ａ－12＜0

この不等式を解くと求めたいａの範囲が出てきます。

－ａ²＋8ａ－12＜0
ａ²－8ａ＋12＞0
(ａ－6)(ａ－2)＞0

よって、ａの範囲は次の通り。

ａ＜2、6＜ａ

(４)の解答：ウ

まずは、二次関数がＸ軸と交わる点の座標を求めます。下の式は（１）で二次関数(イ)を変形させた式です。

Ｙ＝(Ｘ－ａ)²－ａ²＋8ａ－12・・・①

Ｘ軸と交わる点なので、Ｙ＝0となります。よって、上の二次関数の式にＹ＝0を代入します。

0＝(Ｘ－ａ)²－ａ²＋8ａ－12

(Ｘ－ａ)²＝ａ²－8ａ＋12
Ｘ－ａ＝±√ａ²－8ａ＋12
Ｘ＝ａ±√ａ²－8ａ＋12

よって、Ｘ軸と交わる2点の座標は、次の2つになります。

(ａ＋√ａ²－8ａ＋12,0)、(ａ－√ａ²－8ａ＋12,0)

線分ＡＢの長さは、上記2点のＸ座標の差なので以下の式が成り立ちます。

(ａ＋√ａ²－8ａ＋12)－(ａ－√ａ²－8ａ＋12)＝4√3
2√ａ²－8ａ＋12＝4√3
√ａ²－8ａ＋12＝2√3

両辺を2乗してルートを取り除きます。
(√ａ²－8ａ＋12)²＝(2√3)²
ａ²－8ａ＋12＝12
ａ²－8ａ＝0
ａ(ａ－8)＝0

よって、ａ＝0、8

※記載している解説の内容に誤りや不明な点があれば遠慮なくコメントください。