長崎 職業訓練 選考試験問題 数学-問3(平成30年度入校)

試験問題 問３

次の各設問の回答として正しいものをア～エの中から選びなさい。

[１]　図のような円に内接する直角三角形ＡＢＣがある。∠ＡＣＢ＝90°、∠ＢＡＣ＝θ、線分ＢＣ＝ａ、線分ＡＣ＝ｂ、線分ＡＢ＝ｃ のとき、次の各設問に答えなさい。

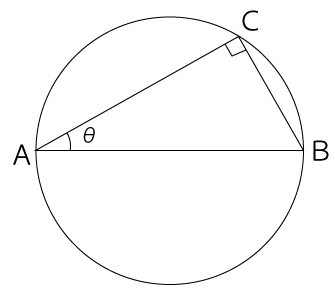
（１）sinθをａ、ｂ、ｃを用いて表しなさい。

（２）θ＝30°、ａ＝5とするとき、外接円の半径を求めなさい。

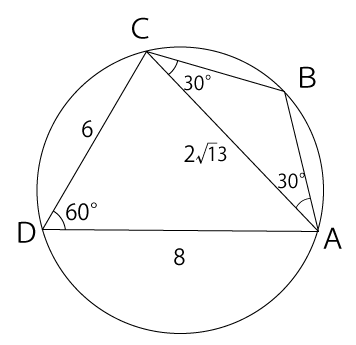
[２]　図のような四角形ＡＢＣＤが円に内接し、∠ＣＤＡ＝60°、∠ＢＣＡ＝30°、線分ＣＤ＝6、線分ＡＤ＝8のとき、次の各設問に答えなさい。

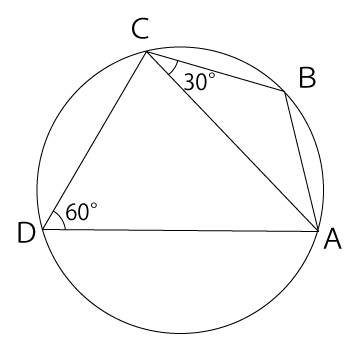
（１）線分ＡＣの長さを求めなさい。

（２）三角形ＡＢＣの面積を求めなさい。

［１］の解答と解説

(１)の解答：イ

この問題は三角比の定義を知っていればすぐに解ける問題です。

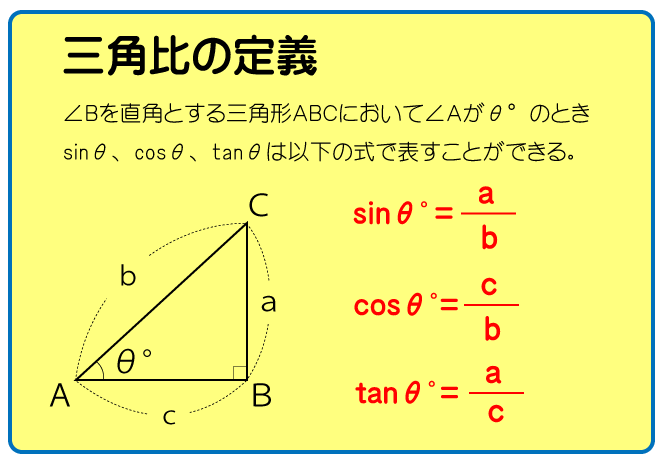
問題の図は下図です。上に記載した三角比の定義のＡＢＣの配置場所が異なるので注意してくださいね。

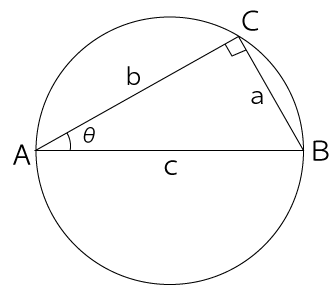
sinθ＝BCAB＝ａｃ

(２)の解答：イ

この問題を解くには、（１）で解説した『三角比の定義』と『タレスの定理』、『三角比(sin30°の値)』を知っている必要があります。

要は、円に内接する三角形の一角が90°の場合、その対辺は必ず円の直径となります。要は、今回の問題であれば辺ＡＢが円の直径となります。よって、まずは、辺ＡＢの長さを求めます。

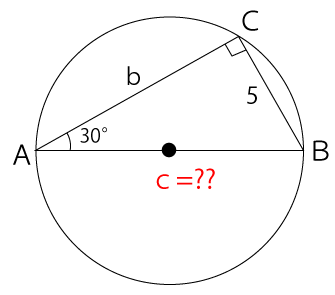
三角比の定義より、以下の式が成り立ちます。

sin30°＝5ｃ

『sin30°＝12』なので辺ｃの長さは次のようになります。

12＝5ｃ

ｃ＝5×2＝10

よって、円の直径である辺ＡＢの長さは10と分かりました。設問で求められてるのは円の半径なので、10÷2＝5

［２］の解答と解説

(１)の解答：エ

点Ｃから辺ＡＤに対して垂線を下ろし、その交点を点Ｅとします。

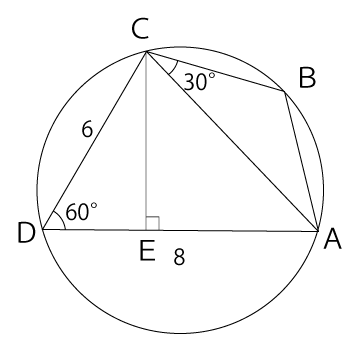
CEの長さは、三角比の定義より次の通りになります。

sin60°＝CEDC
√32＝CE6

CE＝√32×6
CE＝3√3

次にDEの長さを求めます。DEの長さは、三角比の定義より次の通りになります。

cos60°＝DE6
12＝DE6
DE＝3

よって、AEの長さは8-3＝5となります。

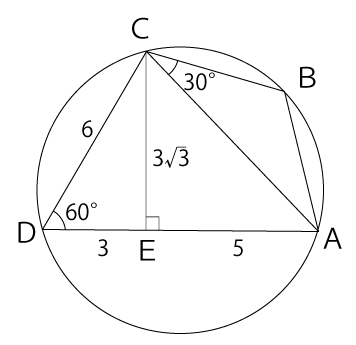
次に辺ACの長さを求めるのですが、三平方の定理を利用します。

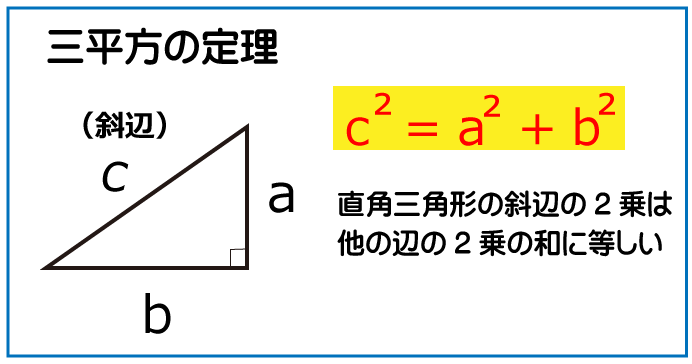
AC²＝CE²＋AE²
AC²＝(3√3)²＋5²
AC²＝27＋25
AC²＝52
AC＝2√13

(２)の解答：ウ

円に内接する四角形の対角の和は必ず180°となります。よって、∠CDA＋∠ABC＝180°となります。

これにより、∠CDA＝60°と分かっているので、∠ABC＝120°となります。よって、∠BAC＝30°となり、三角形ABCは二等辺三角形だと分かります。

点Bから辺ACに垂線を下ろし、その交点を点Fとします。ACの長さは（１）で2√13と分かっています。よって、△ABCは二等辺三角形なのでCFの長さは√13となります。

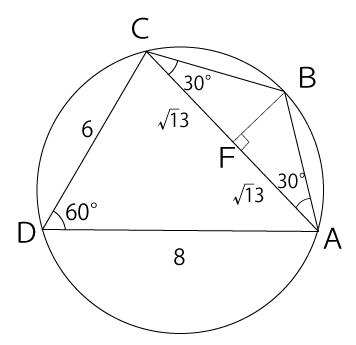
三角比の定義のtanθを利用すればBFの長さが求まります。

tan30°＝BFCF
1√3＝BF√13
BF＝√13√3

よって、△ABCの面積は次の通り。

△ABCの面積＝AC×BF÷2
　　　　　＝2√13×√13√3÷2
　　　　　＝13√3
　　　　　＝13√33

※記載している解説の内容に誤りや不明な点があれば遠慮なくコメントください。