このページは平成30年度入校の長崎県立高等技術専門校(職業訓練校)一般選考試験問題の問4の解答と解説を記載しています。
問1~問4に関しては以下のページに解説をまとめているので参考にして下さい。
実際の試験の問題のPDF用紙は以下のページで確認することができます。
試験問題 問4
空欄に当てはまる数字をマークしなさい。解答は,この問題冊子の表紙を参考に記入しなさい。解答番号は[ツ]~[ニ]
[1] 2次方程式 X²-5X+1=0 の大きい方の解をαとする。α+1αの値は[ツ]
[2] 連立不等式 X²-5X-6<0 、|X-1|>3 を満たすXの値の範囲は[テ]<X<[ト]である。
[3] 0°≦θ≦180° とする。tanθ=2 のとき、cosθの値は [ナ]√[ニ]
解答と解説
[1]の解答:5
解の公式や平方完成を使ってXの解を求めaに代入する方法でも解くことができますが、時間がかかるだけではなく計算ミスも誘発してしまいます。
この問題は、X²-5X+1=0 の式を変形させるだけで解くことができます。
Xの大きい方の解がaなので式にX=aを代入します。
a²-5a+1=0
この式を平方完成と同じようなやり方で α+1α が含まれる形に強引に変形していきます。
両辺をaで割ります。
a-5+1a=0
a+1a=5
[2]の解答:4<X<6
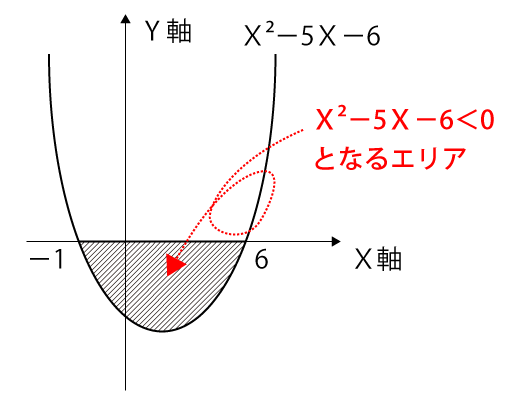
X²-5X-6<0
(X-6)(X+1)<0
-1<X<6・・・①
|X-1|>3
絶対値は絶対値を外すと必ず正の数になるというもの。よって、X-1が元とも正の数であれば問題ないのですが、X-1が負の数の場合、マイナスを掛けて正の数に変換しなければなりません。
X-1が正の数の場合そのまま絶対値が外せる
|X-1|>3
X-1>3
X>4
X-1が負の数の場合マイナスを掛けて正の数に変える
-(X-1)>3
-X+1>3
-X>2
X<-2
よって、Xの取りうる範囲は次の通り。
X>4、X<-2・・・②
①と②の結果を総合してXの取り得る範囲を導きます。
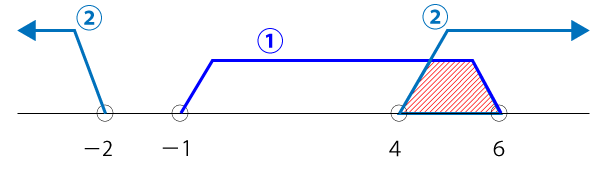
よって、Xの取り得る範囲は次の通り。
4<X<6
[3]の解答:1√5
この問題を解くには三角比の相互関係の公式を知っている必要があります。

今回は公式③を使って解きます。
tan²θ+1=1cos²θ
2²+1=1cos²θ
5=1cos²θ
cos²θ=15
cosθ=1√5
※記載している解説の内容に誤りや不明な点があれば遠慮なくコメントください。

