沖縄 職業訓練 平成25年度 試験問題と解答 問題【２】

平成25年度に沖縄県で実施された職業訓練の選考試験で出題された試験問題と、その解答と解説です。 本ページでは数学問題の設問【２】のみ記載しています。数学問題の設問【１】、【３】～【４】に関しては、次のページを参照してください。

沖縄 職業訓練 平成25年度 試験問題と解答 問題【１】
沖縄 職業訓練 平成25年度 試験問題と解答 問題【３】
沖縄 職業訓練 平成25年度 試験問題と解答 問題【４】

具志川職業能力開発校、浦添職業能力開発校 共通

【２】次の問に答えなさい。

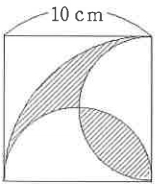
[問題1]　下図において、斜線部分の面積の和を求めなさい。ただし、円周率はΠとして答えること。

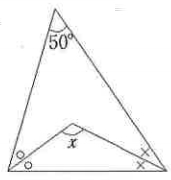
[問題2]　下図において、角Ｘの大きさを求めなさい。

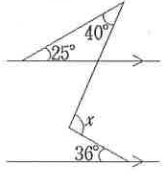
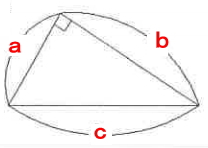
[問題3]　下図において、Ｘの長さを求めなさい。

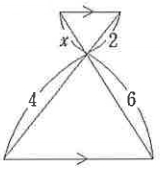
[問題4]　下図において、Ｘの長さを求めなさい。

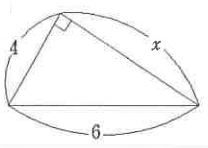
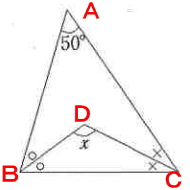
[問題5]　下図において、同じ印をつけた角は等しいとするとき、角Ｘの大きさを求めなさい。

解答と解説

試験問題１の解答：25Π－50
一見難しいように思えますが、パーツごとに分解して計算していくことに気が付けば難しいことはありません。まずは、下図の斜線①の面積を求めます。

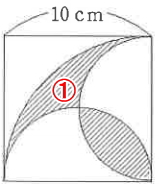
この斜線①を求めるには下図のように図を分解して考えたら簡単ですね。

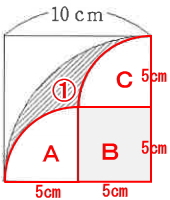
斜線①は、半径10cmの円を1/4にしたもの。ＡとＣは、半径5cmの円を1/4にしたもの。Ｂは、1辺が5cmの正方形。よって、斜線①の面積は、次の式で表すことができます。

　斜線①の面積＝
　(半径10cmの円の面積)/4 － (半径5cmの円の面積)/4 － (半径5cmの円の面積)/4 － 1辺が5cmの正方形の面積

これを実際に計算すると、

　斜線①の面積＝
　(10×10×Π)/4 － (5×5×Π)/4 － (5×5×Π)/4 － (5×5)
　＝25Π － 25Π/4 － 25Π/4 － 25
　＝25Π/2 － 25

次に、斜線②の面積を求めます。

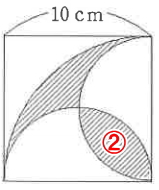
しかし、真面目に斜線②の部分を求めようとすると難しくなるので、まずは、下図のＡの面積を求めます。

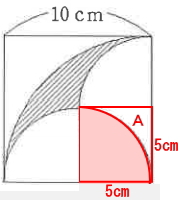
1辺が5cmの正方形の面積から半径5cmの円の1/4の面積を引けば、Ａの面積がでてきます。

　Ａの面積
　Ａの面積＝(5×5)－(5×5×Π÷4)
　　　　　＝25－25Π/4

これでＡの面積が求まりました。次に1辺が5cmの正方形の面積から『Ａの面積×２』を引けば斜線②の面積を求めることができます。

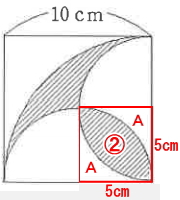
　斜線②の面積＝
　(5×5)－(25－25Π/4)×2
　＝25－50＋25Π/2
　＝25Π/2－25

斜線全体の面積は、斜線①と斜線②の合計なので、

　斜線全体の面積＝(25Π/2 － 25)＋(25Π/2－25)
　　　　　　　　＝25Π－50

試験問題２の解答：101°
下図のように線ａと平行な線ｂを引き、①②③④の順で角度を求めていきます。

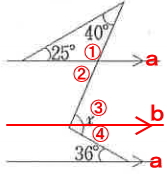
①の角度
三角形の内角の和は180度なので、①の角度は次の通り。

　①の角度＝180－40－25＝115

②の角度
②の角度は、180から①を引いた角度なので次の通り。

　②の角度＝180－115＝65

③の角度
線ａとｂは平行なので、②と③の角度は等しいことになります。よって、③の角度は、65°

④の角度
線ａとｂは平行なので、④の角度は36°とすぐにわかります。

ｒの角度
ｒの角度は、③＋④の角度に等しいので、

　ｒの角度＝65＋36＝101°

試験問題３の解答：３
相似の問題です。

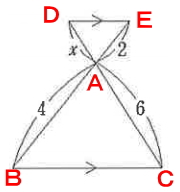
∠ＤＡＥと∠ＢＡＣは、向かい合う角なので等しい。また、辺ＤＥと辺ＢＣは平行なので、∠ＤＥＡと∠ＡＢＣ、∠ＡＤＥと∠ＡＣＢもそれぞれ角度が等しいと分かります。

※補足
図中の『–>—』は、平行を意味します。これを知っていないとこの問題は解けないので覚えておきましょう。

三角形の相似条件の一つに『2組の角度が等しい』というものがあります。要は、三角形なので2組の角度が等しいということは、三角形の3角が等しいというのと同じことですね。よって、三角形ＡＢＣと三角形ＡＥＤも3組の角度が等しいので、この２つの三角形は相似ということが言えます。

辺ＡＢに相似しているのが辺ＡＥ。辺ＡＢの長さが４、辺ＡＥの長さが２なので、相似比は、２：１ だと分かります。

よって、辺ＡＣに相似している辺が辺ＡＤなので、その長さの比も２：１となります。

　辺ＡＣ：辺ＡＤ＝６：Ｘ

比が２：１となるには、辺ＡＣの長さの半分がＸということになります。よって、Ｘの長さは３

　辺ＡＣ：辺ＡＤ＝６：３＝２：１

試験問題４の解答：２√５
中学3年あたりで習う三平方の定理を使用します。これを知っていないとこの問題は解けません。

直角三角形の各辺の長さは、次の式が成り立ちます。(斜辺がｃ)

　ａ²＋ｂ²＝ｃ²

よって、今回の問題の場合、次のようになります。

　ａ²＋ｂ²＝ｃ²
　４²＋Ｘ²＝６²

これを解くと、Ｘの長さが求まります。

　４²＋Ｘ²＝６²
　Ｘ²＝６²－４²
　Ｘ²＝３６－１６
　Ｘ²＝２０
　Ｘ＝√２０
　Ｘ＝√４×５
　Ｘ＝√２²×５
　Ｘ＝２√５

試験問題５の解答：Ｘ＝１１５°
まずは、分かっていることを全て式に置き換えていきましょう。

三角形ＡＢＣは三角形なので内角の和が１８０°となります。よって、次の式が成り立ちます。

　５０＋○＋○＋x＋x＝１８０
　２○＋２x＝１３０
　○＋x＝６５ ・・・(１)

更に三角形ＤＢＣも三角形なので内角の和が１８０°となります。よって、次の式が成り立ちます。

　Ｘ＋○＋x＝１８０

(１)より、○＋x＝６５ と分かっているので、上の式は次のようになります。

　Ｘ＋○＋x＝１８０
　Ｘ＋６５＝１８０
　Ｘ＝１８０－６５
　Ｘ＝１１５

※解説の内容が不明、不十分というのがあればコメントをください。