沖縄 職業訓練 平成25年度 試験問題と解答 問題【４】

平成25年度に沖縄県で実施された職業訓練の選考試験で出題された試験問題と、その解答と解説です。 本ページでは数学問題の設問【４】のみ記載しています。数学問題の設問【１】～【３】に関しては、次のページを参照してください。

沖縄 職業訓練 平成25年度 試験問題と解答 問題【１】
沖縄 職業訓練 平成25年度 試験問題と解答 問題【２】
沖縄 職業訓練 平成25年度 試験問題と解答 問題【３】

具志川職業能力開発校、浦添職業能力開発校 共通

【４】次の問に答えなさい。
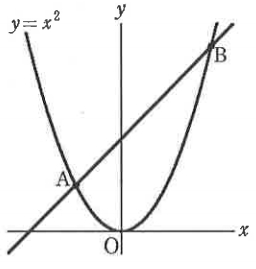
放物線Ｙ＝Ｘ²上に、２点Ａ、ＢをＸ座標がそれぞれ－１、２となるようにとる。また、点Ｐが放物線上のＯとＢの間にあるとする。△ＰＡＢの面積をＳとし、Ｐを通ってＡＢに平行に引いた直線がＹ軸と交わる点(０, ａ)とするとき、次の問に答えなさい。

[問題1]
直線ＡＢの式を求めなさい。

[問題2]
Ｓをａの式で表しなさい。

[問題3]
Ｓ＝３となる点Ｐの位置を求めなさい。

[問題4]
Ｓ＝２７/３となる点Ｐの位置を求めなさい。

解答と解説

試験問題１の解答：Ｙ＝Ｘ＋２
まずは、点Ａと点Ｂの座標をもとめましょう。

点Ａの座標
点ＡのＸ座標は、放物線Ｙ＝Ｘ² 上の点で－１ということなので、Ｙ座標を求めるには放物線の式にＸ＝－１を代入すればよい。
Ｙ＝Ｘ²＝(－１)²＝１

よって、点Ａの座標は(－１, １)

点Ｂの座標
点ＢのＸ座標は、放物線Ｙ＝Ｘ² 上の点で２ということなので、Ｙ座標を求めるには放物線の式にＸ＝２を代入すればよい。
Ｙ＝Ｘ²＝(２)²＝４

よって、点Ｂの座標は(２, ４)

直線ＡＢの式を求める
直線の式をＹ＝ａＸ＋ｂとした場合、この直線は点Ａ(－１, １)と、点Ｂ(２, ４)を通るのでＸとＹの値をそれぞれ代入し、ａとｂの値を求め直線の式を完成させます。

点Ａ(－１, １)を通る事より
Ｙ＝ａＸ＋ｂ
１＝－ａ＋ｂ ・・・(１)

点Ｂ(２, ４)を通る事より
Ｙ＝ａＸ＋ｂ
４＝２ａ＋ｂ ・・・(２)

式(１)(２)ができました。式(１)(２)の左辺どうし、右辺どうしをそれぞれ引き算するとａの値が求まります。
１＝－ａ＋ｂ ・・・(１)
４＝２ａ＋ｂ ・・・(２)

１－４＝(－ａ＋ｂ)－(２ａ＋ｂ)
－３＝－３ａ
ａ＝１

ａの値が求まりました。このａの値を式(１)もしくは式(２)に代入すると残るｂの値も求まります。
１＝－ａ＋ｂ ・・・(１)
１＝－１＋ｂ
ｂ＝２

よって、直線の式Ｙ＝ａＸ＋ｂは、Ｙ＝Ｘ＋２ だと分かります。

試験問題２の解答：(６－３ａ)/２
少々難易度が高い問題です。難易度が高いと言っても難しい計算が必要なわけではなく、ある事に気が付くか気が付かないかの差です。この差は過去に同様の問題を実施していなければ気が付き難いので、今回でしっかり覚えておきましょう。

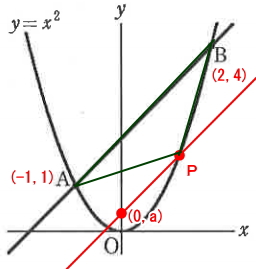
上図のように点Ｐを通る直線がＹ軸と交わる点をＣ点とします。座標は設問にも記載されている通り(０, ａ)です。

求めるのは、三角形ＰＡＢの面積ですが、実は三角形ＰＡＢの面積は三角形ＣＢＡの面積と同じになります。この点が過去に同様の問題をやった人でないと気が付かない点です。では、何故、三角形ＰＡＢと三角形ＣＢＡが同じ面積なのか？

三角形の面積は、『底辺×高さ÷２』ですよね。
三角形ＰＡＢの面積を求める場合、底辺を辺ＡＢとした場合、高さは点Ｐから線分ＡＢに垂直に下ろした線になります。

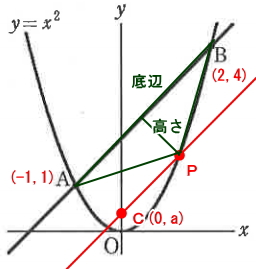
次に三角形ＣＡＢの面積を求める場合、底辺を辺ＡＢとした場合、高さは点Ｃから線分ＡＢに垂直に下ろした線になります。底辺はＡＢで三角形ＰＡＢと共通なので長さは同じ。また、高さも点Ｐを通る直線と直線ＡＢは平行なので、点Ｃから直線ＡＢに垂直に下ろした距離も三角形ＰＡＢの高さと同じになります。

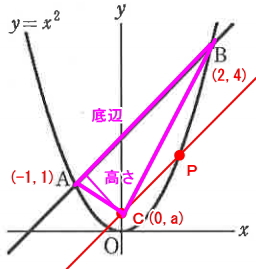
よって、底辺の長さと高さが同じということは、当然、面積も同じことになります。そこで、問題は三角形ＰＡＢの面積を求めるとありますが、三角形ＣＡＢの面積を求めても同じなので三角形ＣＡＢの面積を求めます。

三角形ＣＡＢの面積を求めるには下図のように三角形①②の２つに分離して考えます。

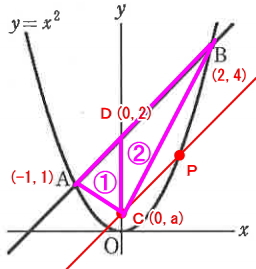
直線ＡＢとＹ軸の交点をＤ(０, ２)とした場合、三角形ＣＡＤと、三角形ＣＢＤの面積は次のようになります。

三角形ＣＡＤの面積
三角形の底辺を辺ＣＤとした場合、高さは点ＡのＸ座標になります。辺ＣＤの長さは、Ｄ点のＹ座標－Ｃ点のＹ座標なので

底辺ＣＤの長さ＝２－ａ
高さ＝１

高さはＡ点のＸ座標ですが、Ｘ座標は－１。しかし、高さが－１というのはおかしい。あくまで長さなのでＸ座標値の絶対値になります。よって、高さは１となります。

三角形ＣＡＤの面積＝(２－ａ)×１÷２
　　　　　　　　　＝(２－ａ)/２

※問い合わせに対する補足

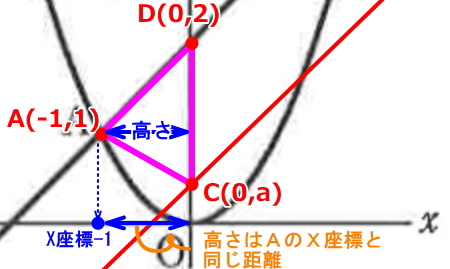
上図のような三角形ＣＡＤがあり、底辺を辺ＣＤとした場合、三角形ＣＡＤの高さは頂点Ａから辺ＣＤに垂直に下ろした線が高さ部分となる。点Ａは、Ｙ座標から－１離れた位置にあり（Ａ点のＸ座標のことですね）、これが三角形ＣＡＤの高さになります。

三角形ＣＢＤの面積
底辺は、三角形ＣＡＤと同じ辺ＣＤ。高さは、点ＢのＸ座標となります。

底辺ＣＤの長さ＝２－ａ
高さ＝２

よって、三角形ＣＢＤの面積は

三角形ＣＢＤの面積＝(２－ａ)×２÷２
　　　　　　　　　＝(２－ａ)

三角形ＡＢＣの面積
三角形ＡＢＣの面積Ｓは、三角形ＣＡＤとＣＢＤの合計なので、

　Ｓ＝(２－ａ)/２＋(２－ａ)
　　＝３(２－ａ)/２
　　＝(６－３ａ)/２

試験問題３の解答：(１, １)
問題２で求めた面積の式を利用します。

　Ｓ＝(６－３ａ)/２

この式にＳ＝３を代入するとａの値が求まります。

　３＝(６－３ａ)/２
　６＝(６－３ａ)
　３ａ＝６－６
　３ａ＝０
　ａ＝０

よって、点Ｐを通る直線は原点(０, ０)を通る直線だとわかります。よって、点Ｐを通る直線の式は、

　Ｙ＝Ｘ

この直線と放物線Ｙ＝Ｘ²が交わる点がＰなので、直線の式を放物線の式に代入し、Ｐ点の座標を求めます。

　Ｙ＝Ｘ² にＹ＝Ｘを代入
　Ｘ＝Ｘ²
　Ｘ²－Ｘ＝０
　Ｘ(Ｘ－１)＝０

よって、Ｘ＝０、１

この時のＹ座標は

　(０, ０) (１, １)

このことより、点Ｐは座標(０, ０)と(１, １)の２ヵ所で交わることがわかります。しかし、座標(０, ０)は原点Ｏのこと。問題では『点Ｐは放物線上のＯとＢの間にある』となっているので、原点(０, ０)は除外。よって、求めたい点Ｐの座標は(１, １)

試験問題４の解答：(１/２, １/４)
問題３と解き方は同じです。

　Ｓ＝(６－３ａ)/２

この式にＳ＝２７/８を代入するとａの値が求まります。

　２７/８＝(６－３ａ)/２
　２７＝４(６－３ａ)
　２７＝２４－１２ａ
　１２ａ＝２４－２７
　ａ＝－１/４

よって、点Ｐを通る直線は点(０, －１/４)を通る直線だとわかります。よって、点Ｐを通る直線の式は、

　Ｙ＝Ｘ－１/４

この直線と放物線Ｙ＝Ｘ²が交わる点がＰなので、直線の式を放物線の式に代入し、Ｐ点の座標を求めます。

　Ｙ＝Ｘ² にＹ＝Ｘ－１/４を代入
　Ｘ－１/４＝Ｘ²
　Ｘ²－Ｘ＋１/４＝０
　４Ｘ²－４Ｘ＋１＝０
　(２Ｘ－１)²＝０

よって、Ｘ＝１/２

この時のＹ座標は

　Ｙ＝Ｘ²
　Ｙ＝(１/２)²
　　＝１/４

よって、求めたい点Ｐの座標は(１/２, １/４)

※解説の内容が不明、不十分というのがあればコメントをください。